In the previous section, we saw gravitational potential
• In this section we will see Escape velocity
1. In fig.8.47 below, an object of mass m is being launched from the surface of the earth
• Let the initial velocity be vi
• Then the initial kinetic energy Ki = $\mathbf\small{\frac{1}{2}mv_i^2}$
2. We already know the initial potential energy Ui
• That is., the potential energy when the object is at the surface of the earth
• It is given by: Ui = $\mathbf\small{-\frac{G\,M_E\,m}{R_E}}$
3. So the initial total energy = Ki + Ui = $\mathbf\small{\frac{1}{2}mv_i^2-\frac{G\,M_E\,m}{R_E}}$
4. Now we want the final values
• We want the object to escape from the gravitational field of the earth
• We know that, as the object rises, the speed goes on decreasing
♦ If vi is large the object will rise to a larger height
♦ If vi is small, the object will rise only to a smaller height
♦ If vi is large enough, the object will rise to such a height that, it is out of the gravitational field
• The height at which the object is out of the gravitational field is our final position. This is shown in fig.8.48 below:
5. If vi is more than 'what is sufficient', the object will continue to rise even after escaping from the field
• We do not want this to happen. What we want is to ‘just escape’. We do not want the object to travel further
6. That means, at the instant when the object is out of the field, the velocity must be zero
• This implies that, at the instant when the object is out of the field, the kinetic energy must be zero
7. We can write:
At the final position, vf = 0 ⇒ Kf = 0
8. There is also another implication arising from 'just escape'. We can write it in 6 steps:
(i) If the initial velocity vi is more than ‘what is sufficient’, the object will travel further even after getting out of the field
(ii) We do not want this to happen. We want to ‘just escape’
(iii) So vi must be just equal to ‘what is sufficient’ to ‘just escape’
(iv) We call that velocity: The escape velocity
• It is denoted as ve
(v) The initial velocity vi must be equal to ve. So we can write:
Initial kinetic energy Ki = $\mathbf\small{\frac{1}{2}mv_e^2}$
(vi) Thus from (3), we get:
Total initial energy = Ki + Ui = $\mathbf\small{\frac{1}{2}mv_e^2-\frac{G\,M_E\,m}{R_E}}$
9. Next we calculate the potential energy at the final instant
• The ‘instant when the object is out of the field’ implies that, at that instant, there is no influence of the field
• We will have a potential energy only if there is an influence of the field
• So at the final position, there is no potential energy
That is., Uf = 0
10. Thus using the results in (7) and (9), we can write:
Total energy at the final point = (Kf + Uf) = (0 + 0) = 0
11. The total initial energy must be equal to the total final energy
• Using the results in (8) and (10), we get: $\mathbf\small{\frac{1}{2}mv_e^2-\frac{G\,M_E\,m}{R_E}=0}$
$\mathbf\small{\Rightarrow \frac{1}{2}v_e^2=\frac{G\,M_E}{R_E}}$
• Thus we get: Eq.8.17: $\mathbf\small{v_e=\sqrt{\frac{2G\,M_E}{R_E}}}$
12. Multiplying both numerator and denominator by √RE, we get: $\mathbf\small{v_e=\sqrt{\frac{2G\,M_E\,R_E}{R_E^2}}}$
• Thus we get: Eq.8.18: $\mathbf\small{v_e=\sqrt{2gR_E}}$
(∵ $\mathbf\small{\frac{2G\,M_E}{R_E^2}=g}$)
13. Inputting the values in Eq.8.18, we get:
$\mathbf\small{v_e=\sqrt{2\times 9.81 \times 6.371 \times 10^6}=11.18 \times 10^3}$ ms-1
14. An important note:
• Throw some thing upwards with initial velocity ve
♦ It will escape from the gravitational field of the earth
♦ It will escape without any need for 'propulsion by burning fuel'
• Throw some thing upwards with initial velocity less than ve
♦ It will escape only if 'propulsion by burning fuel' is supplied
15. Eq.8.17 shows that, the escape velocity depends only on the mass and radius of the earth
We can write the escape velocity for any planet P:
Eq.8.19: $\mathbf\small{v_{e(P)}=\sqrt{\frac{2G\,M_P}{R_P}}}$
Where:
♦ $\mathbf\small{v_{e(P)}}$ is the escape velocity of the planet P
♦ $\mathbf\small{M_P}$ is the mass of the planet P
♦ $\mathbf\small{R_P}$ is the radius of the planet P
Solved example 8.33
Calculate the escape velocity from the surface of a planet of mass 14.8 × 1022 kg. Radius of the planet is 3.48 × 106 m
Solution:
• We have Eq.8.19: $\mathbf\small{v_{e(P)}=\sqrt{\frac{2G\,M_P}{R_P}}}$
• Substituting the values, we get:
$\mathbf\small{v_{e(P)}=\sqrt{\frac{2\times 6.67 \times 10^{-11}\times 14.8 \times 10^{22}}{3.48 \times 10^{6}}}}$ = 2381.9 m s-1 = 2.38 km s-1
Solved example 8.34
Mass of Jupiter is 318 times the mass of earth. Radius of Jupiter is 11.2 times the radius of earth. If the escape velocity of earth is 11.2 km s-1, calculate the escape velocity of Jupiter
Solution:
1. For earth, we have: $\mathbf\small{v_{e(E)}=\sqrt{\frac{2G\,M_E}{R_E}}}$
• For Jupiter, we have: $\mathbf\small{v_{e(J)}=\sqrt{\frac{2G\,M_J}{R_J}}}$
2. Taking ratio of squares, we get:
$\mathbf\small{\frac{v_{e(E)}^2}{v_{e(J)}^2}=\frac{2G\,M_E}{R_E}\times \frac{R_J}{2G\,M_J}=\frac{M_E}{M_J}\times \frac{R_J}{R_E}}$
$\mathbf\small{\Rightarrow \frac{v_{e(E)}^2}{v_{e(J)}^2}=\frac{M_E}{318M_E}\times \frac{11.2R_E}{R_E}=\frac{11.2}{318}}$
$\mathbf\small{\Rightarrow v_{e(J)}^2=\frac{318}{11.2}v_{e(E)}^2}$
$\mathbf\small{\Rightarrow v_{e(J)}^2=\frac{318}{11.2}\times 11.2^2=318 \times 11.2=3561.6}$
$\mathbf\small{\Rightarrow v_{e(J)}=\sqrt{3561.6}=59.7}$ km s-1
Solved example 8.35
The earth is assumed to be a sphere of radius RE. A platform is arranged at a height of RE from the surface of the earth. The escape velocity of a body from this platform is (k×ve). Where ve is the escape velocity from the surface of the earth. Find the value of k
Solution:
1. The platform is at a distance of 2RE from the center of the earth
• So potential energy of the body when it is on the platform = $\mathbf\small{-\frac{GM_Em}{2R_E}}$
• Where m is the mass of the body
2. The body is launched with an initial velocity of kve from the platform
• So kinetic energy of the body when it is at the platform = $\mathbf\small{\frac{1}{2}m(kv_e)^2=\frac{1}{2}mk^2v_e^2}$
3. So total energy at the platform = $\mathbf\small{-\frac{GM_Em}{2R_E}+\frac{1}{2}mk^2v_e^2}$
4. Total energy when the body has just escaped from earth's gravitational field = 0
5. Applying law of conservation of energy, the results in (3) and (4) must be equal
• So we can write: $\mathbf\small{-\frac{GM_Em}{2R_E}+\frac{1}{2}mk^2v_e^2=0}$
$\mathbf\small{\Rightarrow -\frac{GM_E}{R_E}+k^2v_e^2=0}$
$\mathbf\small{\Rightarrow \frac{GM_E}{R_E}=k^2v_e^2}$
6. Multiplying the numerator and denominator of the left side by 2, we get:
$\mathbf\small{\frac{2GM_E}{2R_E}=k^2v_e^2}$
$\mathbf\small{\Rightarrow \frac{v_e^2}{2}=k^2v_e^2}$
(∵ $\mathbf\small{\frac{2GM_E}{R_E}=v_e^2}$)
$\mathbf\small{\Rightarrow \frac{1}{2}=k^2}$
$\mathbf\small{\Rightarrow k=\frac{1}{\sqrt{2}}}$
Solved example 8.36
We know that, to escape from the gravitational field of the earth, a body must be given a 'minimum initial kinetic energy'. Which of the following is equal to that kinetic energy?
$\mathbf\small{\frac{mgR_E}{2},\;2mgR_E\;,\;mgR_E\;,\;\frac{3mgR_E}{2}}$
Solution:
1. The 'minimum initial kinetic energy' will be equal to $\mathbf\small{\frac{1}{2}mv_e^2}$
2. But ve is equal to $\mathbf\small{\sqrt{2gR_E}}$
3. Substituting in (1), we get:
'Minimum initial kinetic energy' = $\mathbf\small{\frac{1}{2}m(\sqrt{2gR_E})^2}$
= $\mathbf\small{\frac{1}{2}m \times(2gR_E)=mgR_E}$
Solved example 8.37
Two uniform solid spheres of equal radii R, but mass M and 4 M have a center to center separation 6R, as shown in fig. 8.49(a). The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. Obtain an expression for the minimum initial speed vi of the projectile so that it reaches the surface of the second sphere
Solution:
1. The mass M will exert an attractive force on m
• The magnitude of this attractive force will be $\mathbf\small{\frac{GMm}{r^2}}$
♦ Where r is the distance of m from the center of M
♦ This is shown in fig.b
• This force acts towards the left
2. The mass 4M will also exert an attractive force on m
• The magnitude of this attractive force will be $\mathbf\small{\frac{4GMm}{(6R-r)^2}}$
♦ Where r is the distance of m from the center of 4M
• This force acts towards the right
3. The two forces act in opposite directions
The magnitudes of the forces depend on the value of r
4. Let the magnitudes become equal when the m is at N
• Then we have: $\mathbf\small{\frac{GMm}{r^2}=\frac{4GMm}{(6R-r)^2}}$
$\mathbf\small{\Rightarrow \frac{1}{r^2}=\frac{4}{(6R-r)^2}}$
$\mathbf\small{\Rightarrow \frac{1}{r}=\frac{\pm 2}{(6R-r)}}$
• Solving this equation, we get: r = 2R or -6R
• For our present problem, -6R is not acceptable. So we take r = 2R
• We can write: At N, the mass m will experience a zero net force
5. Our aim is to make the mass m to reach N
• We must be able to accomplish this by supplying the 'least possible' external energy
6. The external energy is in the form of kinetic energy
• So we can write:
We must be able to accomplish the task in (5) using the 'least possible' launch velocity
• The launch velocity is the initial velocity vi
• So we must find the least possible vi so that, m will 'just reach' N
• 'Just reach' indicates that, the velocity of m will be zero when it reaches N
7. So the velocity of m will become zero when it reaches N
• Even though the velocity becomes zero, when it reaches N, the larger mass 4M will pull the mass and so, the m can reach 4M
8. Thus we can write:
The kinetic energy at N is zero
9. We will consider the journey from M to N
• Ki and Ui are the energies of m when it is at the surface of M
• Kf and Uf are the energies of m when it is at N
10. Next, we will write the values of those energies:
• We have: Ki = $\mathbf\small{\frac{1}{2}mv_i^2}$
• Ui will be the sum of two items:
♦ Contribution from M
♦ Contribution from 4M
• So we get: Ui = $\mathbf\small{-\frac{GMm}{R}+-\frac{4GMm}{5R}}$
The answer can be written in 4 steps:
(i) The 4M mass creates a 'gravitational potential' around itself in all directions
(We have seen the details in the previous section)
(ii) At a distance of 5R, this potential is equal to $\mathbf\small{-\frac{4GM}{5R}}$
(iii) This is the potential experienced by unit mass
(iv) So a mass m will experience a potential of $\mathbf\small{-\frac{4GMm}{5R}}$
• In this section we will see Escape velocity
1. In fig.8.47 below, an object of mass m is being launched from the surface of the earth
 |
| Fig.8.47 |
• Then the initial kinetic energy Ki = $\mathbf\small{\frac{1}{2}mv_i^2}$
2. We already know the initial potential energy Ui
• That is., the potential energy when the object is at the surface of the earth
• It is given by: Ui = $\mathbf\small{-\frac{G\,M_E\,m}{R_E}}$
3. So the initial total energy = Ki + Ui = $\mathbf\small{\frac{1}{2}mv_i^2-\frac{G\,M_E\,m}{R_E}}$
4. Now we want the final values
• We want the object to escape from the gravitational field of the earth
• We know that, as the object rises, the speed goes on decreasing
♦ If vi is large the object will rise to a larger height
♦ If vi is small, the object will rise only to a smaller height
♦ If vi is large enough, the object will rise to such a height that, it is out of the gravitational field
• The height at which the object is out of the gravitational field is our final position. This is shown in fig.8.48 below:
 |
| Fig.8.48 |
• We do not want this to happen. What we want is to ‘just escape’. We do not want the object to travel further
6. That means, at the instant when the object is out of the field, the velocity must be zero
• This implies that, at the instant when the object is out of the field, the kinetic energy must be zero
7. We can write:
At the final position, vf = 0 ⇒ Kf = 0
8. There is also another implication arising from 'just escape'. We can write it in 6 steps:
(i) If the initial velocity vi is more than ‘what is sufficient’, the object will travel further even after getting out of the field
(ii) We do not want this to happen. We want to ‘just escape’
(iii) So vi must be just equal to ‘what is sufficient’ to ‘just escape’
(iv) We call that velocity: The escape velocity
• It is denoted as ve
(v) The initial velocity vi must be equal to ve. So we can write:
Initial kinetic energy Ki = $\mathbf\small{\frac{1}{2}mv_e^2}$
(vi) Thus from (3), we get:
Total initial energy = Ki + Ui = $\mathbf\small{\frac{1}{2}mv_e^2-\frac{G\,M_E\,m}{R_E}}$
9. Next we calculate the potential energy at the final instant
• The ‘instant when the object is out of the field’ implies that, at that instant, there is no influence of the field
• We will have a potential energy only if there is an influence of the field
• So at the final position, there is no potential energy
That is., Uf = 0
10. Thus using the results in (7) and (9), we can write:
Total energy at the final point = (Kf + Uf) = (0 + 0) = 0
11. The total initial energy must be equal to the total final energy
• Using the results in (8) and (10), we get: $\mathbf\small{\frac{1}{2}mv_e^2-\frac{G\,M_E\,m}{R_E}=0}$
$\mathbf\small{\Rightarrow \frac{1}{2}v_e^2=\frac{G\,M_E}{R_E}}$
• Thus we get: Eq.8.17: $\mathbf\small{v_e=\sqrt{\frac{2G\,M_E}{R_E}}}$
12. Multiplying both numerator and denominator by √RE, we get: $\mathbf\small{v_e=\sqrt{\frac{2G\,M_E\,R_E}{R_E^2}}}$
• Thus we get: Eq.8.18: $\mathbf\small{v_e=\sqrt{2gR_E}}$
(∵ $\mathbf\small{\frac{2G\,M_E}{R_E^2}=g}$)
13. Inputting the values in Eq.8.18, we get:
$\mathbf\small{v_e=\sqrt{2\times 9.81 \times 6.371 \times 10^6}=11.18 \times 10^3}$ ms-1
14. An important note:
• Throw some thing upwards with initial velocity ve
♦ It will escape from the gravitational field of the earth
♦ It will escape without any need for 'propulsion by burning fuel'
• Throw some thing upwards with initial velocity less than ve
♦ It will escape only if 'propulsion by burning fuel' is supplied
15. Eq.8.17 shows that, the escape velocity depends only on the mass and radius of the earth
We can write the escape velocity for any planet P:
Eq.8.19: $\mathbf\small{v_{e(P)}=\sqrt{\frac{2G\,M_P}{R_P}}}$
Where:
♦ $\mathbf\small{v_{e(P)}}$ is the escape velocity of the planet P
♦ $\mathbf\small{M_P}$ is the mass of the planet P
♦ $\mathbf\small{R_P}$ is the radius of the planet P
Now we will see some solved examples
Calculate the escape velocity from the surface of a planet of mass 14.8 × 1022 kg. Radius of the planet is 3.48 × 106 m
Solution:
• We have Eq.8.19: $\mathbf\small{v_{e(P)}=\sqrt{\frac{2G\,M_P}{R_P}}}$
• Substituting the values, we get:
$\mathbf\small{v_{e(P)}=\sqrt{\frac{2\times 6.67 \times 10^{-11}\times 14.8 \times 10^{22}}{3.48 \times 10^{6}}}}$ = 2381.9 m s-1 = 2.38 km s-1
Solved example 8.34
Mass of Jupiter is 318 times the mass of earth. Radius of Jupiter is 11.2 times the radius of earth. If the escape velocity of earth is 11.2 km s-1, calculate the escape velocity of Jupiter
Solution:
1. For earth, we have: $\mathbf\small{v_{e(E)}=\sqrt{\frac{2G\,M_E}{R_E}}}$
• For Jupiter, we have: $\mathbf\small{v_{e(J)}=\sqrt{\frac{2G\,M_J}{R_J}}}$
2. Taking ratio of squares, we get:
$\mathbf\small{\frac{v_{e(E)}^2}{v_{e(J)}^2}=\frac{2G\,M_E}{R_E}\times \frac{R_J}{2G\,M_J}=\frac{M_E}{M_J}\times \frac{R_J}{R_E}}$
$\mathbf\small{\Rightarrow \frac{v_{e(E)}^2}{v_{e(J)}^2}=\frac{M_E}{318M_E}\times \frac{11.2R_E}{R_E}=\frac{11.2}{318}}$
$\mathbf\small{\Rightarrow v_{e(J)}^2=\frac{318}{11.2}v_{e(E)}^2}$
$\mathbf\small{\Rightarrow v_{e(J)}^2=\frac{318}{11.2}\times 11.2^2=318 \times 11.2=3561.6}$
$\mathbf\small{\Rightarrow v_{e(J)}=\sqrt{3561.6}=59.7}$ km s-1
Solved example 8.35
The earth is assumed to be a sphere of radius RE. A platform is arranged at a height of RE from the surface of the earth. The escape velocity of a body from this platform is (k×ve). Where ve is the escape velocity from the surface of the earth. Find the value of k
Solution:
1. The platform is at a distance of 2RE from the center of the earth
• So potential energy of the body when it is on the platform = $\mathbf\small{-\frac{GM_Em}{2R_E}}$
• Where m is the mass of the body
2. The body is launched with an initial velocity of kve from the platform
• So kinetic energy of the body when it is at the platform = $\mathbf\small{\frac{1}{2}m(kv_e)^2=\frac{1}{2}mk^2v_e^2}$
3. So total energy at the platform = $\mathbf\small{-\frac{GM_Em}{2R_E}+\frac{1}{2}mk^2v_e^2}$
4. Total energy when the body has just escaped from earth's gravitational field = 0
5. Applying law of conservation of energy, the results in (3) and (4) must be equal
• So we can write: $\mathbf\small{-\frac{GM_Em}{2R_E}+\frac{1}{2}mk^2v_e^2=0}$
$\mathbf\small{\Rightarrow -\frac{GM_E}{R_E}+k^2v_e^2=0}$
$\mathbf\small{\Rightarrow \frac{GM_E}{R_E}=k^2v_e^2}$
6. Multiplying the numerator and denominator of the left side by 2, we get:
$\mathbf\small{\frac{2GM_E}{2R_E}=k^2v_e^2}$
$\mathbf\small{\Rightarrow \frac{v_e^2}{2}=k^2v_e^2}$
(∵ $\mathbf\small{\frac{2GM_E}{R_E}=v_e^2}$)
$\mathbf\small{\Rightarrow \frac{1}{2}=k^2}$
$\mathbf\small{\Rightarrow k=\frac{1}{\sqrt{2}}}$
Solved example 8.36
We know that, to escape from the gravitational field of the earth, a body must be given a 'minimum initial kinetic energy'. Which of the following is equal to that kinetic energy?
$\mathbf\small{\frac{mgR_E}{2},\;2mgR_E\;,\;mgR_E\;,\;\frac{3mgR_E}{2}}$
Solution:
1. The 'minimum initial kinetic energy' will be equal to $\mathbf\small{\frac{1}{2}mv_e^2}$
2. But ve is equal to $\mathbf\small{\sqrt{2gR_E}}$
3. Substituting in (1), we get:
'Minimum initial kinetic energy' = $\mathbf\small{\frac{1}{2}m(\sqrt{2gR_E})^2}$
= $\mathbf\small{\frac{1}{2}m \times(2gR_E)=mgR_E}$
Solved example 8.37
Two uniform solid spheres of equal radii R, but mass M and 4 M have a center to center separation 6R, as shown in fig. 8.49(a). The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. Obtain an expression for the minimum initial speed vi of the projectile so that it reaches the surface of the second sphere
 |
| Fig.8.49 |
1. The mass M will exert an attractive force on m
• The magnitude of this attractive force will be $\mathbf\small{\frac{GMm}{r^2}}$
♦ Where r is the distance of m from the center of M
♦ This is shown in fig.b
• This force acts towards the left
2. The mass 4M will also exert an attractive force on m
• The magnitude of this attractive force will be $\mathbf\small{\frac{4GMm}{(6R-r)^2}}$
♦ Where r is the distance of m from the center of 4M
• This force acts towards the right
3. The two forces act in opposite directions
The magnitudes of the forces depend on the value of r
4. Let the magnitudes become equal when the m is at N
• Then we have: $\mathbf\small{\frac{GMm}{r^2}=\frac{4GMm}{(6R-r)^2}}$
$\mathbf\small{\Rightarrow \frac{1}{r^2}=\frac{4}{(6R-r)^2}}$
$\mathbf\small{\Rightarrow \frac{1}{r}=\frac{\pm 2}{(6R-r)}}$
• Solving this equation, we get: r = 2R or -6R
• For our present problem, -6R is not acceptable. So we take r = 2R
• We can write: At N, the mass m will experience a zero net force
5. Our aim is to make the mass m to reach N
• We must be able to accomplish this by supplying the 'least possible' external energy
6. The external energy is in the form of kinetic energy
• So we can write:
We must be able to accomplish the task in (5) using the 'least possible' launch velocity
• The launch velocity is the initial velocity vi
• So we must find the least possible vi so that, m will 'just reach' N
• 'Just reach' indicates that, the velocity of m will be zero when it reaches N
7. So the velocity of m will become zero when it reaches N
• Even though the velocity becomes zero, when it reaches N, the larger mass 4M will pull the mass and so, the m can reach 4M
8. Thus we can write:
The kinetic energy at N is zero
9. We will consider the journey from M to N
• Ki and Ui are the energies of m when it is at the surface of M
• Kf and Uf are the energies of m when it is at N
10. Next, we will write the values of those energies:
• We have: Ki = $\mathbf\small{\frac{1}{2}mv_i^2}$
• Ui will be the sum of two items:
♦ Contribution from M
♦ Contribution from 4M
• So we get: Ui = $\mathbf\small{-\frac{GMm}{R}+-\frac{4GMm}{5R}}$
• Why do we say that the contribution from 4M is $\mathbf\small{-\frac{4GMm}{5R}}$?
(i) The 4M mass creates a 'gravitational potential' around itself in all directions
(We have seen the details in the previous section)
(ii) At a distance of 5R, this potential is equal to $\mathbf\small{-\frac{4GM}{5R}}$
(iii) This is the potential experienced by unit mass
(iv) So a mass m will experience a potential of $\mathbf\small{-\frac{4GMm}{5R}}$
11. So total initial energy = Ki + Ui = $\mathbf\small{\frac{1}{2}mv_i^2-\frac{GMm}{R}-\frac{4GMm}{5R}}$
12. Next we take up the final energies
We know that Uf = 0
13. Uf will be the sum of two items:
♦ Contribution from M
♦ Contribution from 4M
• So we get: Uf = $\mathbf\small{-\frac{GMm}{2R}+-\frac{4GMm}{4R}}$
14. So total final energy = Kf + Uf = $\mathbf\small{0-\frac{GMm}{2R}-\frac{4GMm}{4R}}$
15. The results in (11) and (14) must be equal. So we can write:
$\mathbf\small{\frac{1}{2}mv_i^2-\frac{GMm}{R}-\frac{4GMm}{5R}=\frac{GMm}{2R}-\frac{4GMm}{4R}}$
• Dividing both sides by m, we get:
$\mathbf\small{\frac{1}{2}v_i^2-\frac{GM}{R}-\frac{4GM}{5R}=\frac{GM}{2R}-\frac{4GM}{4R}}$
• The denominators of the GM⁄R terms are 1, 2, 4 and 5. The LCM is 20
• Multiplying both numerators and denominators of those terms by 20, we get:
$\mathbf\small{\frac{1}{2}v_i^2-\frac{20GM}{20R}-\frac{16GM}{20R}=-\frac{10GM}{20R}-\frac{20GM}{20R}}$
$\mathbf\small{\Rightarrow \frac{1}{2}v_i^2=\frac{6GM}{20R}}$
$\mathbf\small{\Rightarrow v_i^2=\frac{3GM}{5R}}$
$\mathbf\small{\Rightarrow v_i=\sqrt{\frac{3GM}{5R}}}$
1. Escape velocity does not depend on the angle of projection. That is., the direction of the velocity vector is not important.
• This is because, we are considering only the 'kinetic energy due to the velocity'
• But most rockets are launched towards the east direction
• The reason can be explained using fig.8.50 below:
(i) The blue sphere represents the earth. The yellow line is the axis
(ii) The direction of spin is indicated by the curved arrow. This curved arrow points towards the east
• That is., the earth spins towards the east
(iv) So a rocket is launched towards the east. This will give an additional velocity to the rocket
2. From Eq.8.17, we see that, the escape velocity depends upon mass and radius. G is an universal constant
• So value of escape velocity is different for different planets
3. Different molecules in the gaseous atmosphere will be having different velocities. We take an average velocity for calculations. This average velocity is called 'root mean square velocity'.
(i) Consider any planet
(ii) Note down the root mean square velocity of the molecules in the atmosphere of that planet
(iii) If this velocity is less than the escape velocity of that planet, the molecules cannot escape
(iv) In that case, an atmosphere will be present for that planet
• For moon, the escape velocity is very low: 2.3 km s-1
♦ So the molecules are able to escape into space, leaving the moon with no atmosphere
• For Jupiter, the escape velocity is very high: 60 km s-1
♦ So the molecules are not able to escape. Jupiter has a thick atmosphere
4. We saw that, escape velocity is the initial velocity at the time of launch from the surface of planet
(i) As the object rises, it's velocity decreases
(ii) Finally, when it reaches outer space where there is no influence of gravity, the velocity becomes zero
• The revers steps are also true:
• Drop an object from outer space where there is no influence of gravity
('Drop' indicates that initial velocity is zero)
(i) As the objects descends, the velocity increases
(ii) Finally, when it hits the surface, the velocity will be equal to the escape velocity
5. In calculating the escape velocity, 'air resistance' and 'gravitational effect due to other celestial bodies' are neglected
12. Next we take up the final energies
We know that Uf = 0
13. Uf will be the sum of two items:
♦ Contribution from M
♦ Contribution from 4M
• So we get: Uf = $\mathbf\small{-\frac{GMm}{2R}+-\frac{4GMm}{4R}}$
14. So total final energy = Kf + Uf = $\mathbf\small{0-\frac{GMm}{2R}-\frac{4GMm}{4R}}$
15. The results in (11) and (14) must be equal. So we can write:
$\mathbf\small{\frac{1}{2}mv_i^2-\frac{GMm}{R}-\frac{4GMm}{5R}=\frac{GMm}{2R}-\frac{4GMm}{4R}}$
• Dividing both sides by m, we get:
$\mathbf\small{\frac{1}{2}v_i^2-\frac{GM}{R}-\frac{4GM}{5R}=\frac{GM}{2R}-\frac{4GM}{4R}}$
• The denominators of the GM⁄R terms are 1, 2, 4 and 5. The LCM is 20
• Multiplying both numerators and denominators of those terms by 20, we get:
$\mathbf\small{\frac{1}{2}v_i^2-\frac{20GM}{20R}-\frac{16GM}{20R}=-\frac{10GM}{20R}-\frac{20GM}{20R}}$
$\mathbf\small{\Rightarrow \frac{1}{2}v_i^2=\frac{6GM}{20R}}$
$\mathbf\small{\Rightarrow v_i^2=\frac{3GM}{5R}}$
$\mathbf\small{\Rightarrow v_i=\sqrt{\frac{3GM}{5R}}}$
Now we know the basics about escape velocity. We must always keep the following 5 points in mind:
• This is because, we are considering only the 'kinetic energy due to the velocity'
• But most rockets are launched towards the east direction
• The reason can be explained using fig.8.50 below:
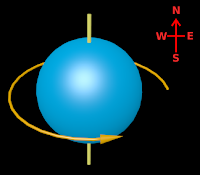 |
| Fig.8.50 |
(ii) The direction of spin is indicated by the curved arrow. This curved arrow points towards the east
• That is., the earth spins towards the east
(iv) So a rocket is launched towards the east. This will give an additional velocity to the rocket
2. From Eq.8.17, we see that, the escape velocity depends upon mass and radius. G is an universal constant
• So value of escape velocity is different for different planets
3. Different molecules in the gaseous atmosphere will be having different velocities. We take an average velocity for calculations. This average velocity is called 'root mean square velocity'.
(i) Consider any planet
(ii) Note down the root mean square velocity of the molecules in the atmosphere of that planet
(iii) If this velocity is less than the escape velocity of that planet, the molecules cannot escape
(iv) In that case, an atmosphere will be present for that planet
• For moon, the escape velocity is very low: 2.3 km s-1
♦ So the molecules are able to escape into space, leaving the moon with no atmosphere
• For Jupiter, the escape velocity is very high: 60 km s-1
♦ So the molecules are not able to escape. Jupiter has a thick atmosphere
4. We saw that, escape velocity is the initial velocity at the time of launch from the surface of planet
(i) As the object rises, it's velocity decreases
(ii) Finally, when it reaches outer space where there is no influence of gravity, the velocity becomes zero
• The revers steps are also true:
• Drop an object from outer space where there is no influence of gravity
('Drop' indicates that initial velocity is zero)
(i) As the objects descends, the velocity increases
(ii) Finally, when it hits the surface, the velocity will be equal to the escape velocity
5. In calculating the escape velocity, 'air resistance' and 'gravitational effect due to other celestial bodies' are neglected
• In the next section we will see what happens if the speed of launch is greater than or less than the escape velocity
No comments:
Post a Comment