In the previous section, we completed a discussion on cross products. In this section we will see angular velocity
We have seen the characteristics of rotational motion in a previous section of this chapter (Details here)
There we saw this:
1. Every particle of the body, which lies on the axis will be stationary
2. Each of the other particles will be rotating in it's own circular path
♦ The center of that circular path lies on the axis
♦ Radius of that circular path = Perpendicular distance of the particle from the axis
3. That circular path lies on a plane
♦ This plane is perpendicular to the axis
• That 'single particle' is shown as a small red sphere in fig.7.76 below:
• The direction of rotation is indicated by the yellow curved arrow
2. At the instant when the reading in the stop watch is 't1', the particle is at A
♦ The linear velocity of the particle at that instant is $\mathbf\small{\vec{v}_{(t1)}}$
♦ It is tangential to the circular path
♦ It is shown in magenta color
• At the instant when the reading in the stop watch is 't2', the particle is at B
♦ The linear velocity of the particle at that instant is $\mathbf\small{\vec{v}_{(t2)}}$
♦ It is tangential to the circular path
♦ It is shown in magenta color
3. The time elapsed between the two instants = Δt = (t2-t1)
• During this time interval Δt, the particle turns through ∠AOB
• We will denote this ∠AOB as Δθ.
4. We know that $\mathbf\small{\text{Linear velocity}=\frac{\text{Displacement}}{time}}$
• In a similar way, $\mathbf\small{\text{Angular velocity}=\frac{\text{Angular displacement}}{time}}$
• So we can write:
The angular velocity with which the particle travels from A to B = $\mathbf\small{\frac{\Delta \theta}{\Delta t}}$
5. But the rotation may not be uniform. That is., angular velocity may be different at different instances
• In such a situation, the the result obtained in (4) will be the 'average angular velocity'
6. If we make the time interval Δt smaller and smaller, it will tend to become zero
• If Δt is very close to zero, we can call it an instant
• Then the result obtained in (4) will be the 'instantaneous angular velocity'
(Note that, Δt must not become exact zero. Then we do not have an instant. Besides, division by zero is undefined)
• The evaluation of 'instantaneous angular velocity' when Δt is very small, can be easily done using calculus
The formula is: $\mathbf\small{\text{Instantaneous angular velocity}=\frac{d\theta}{dt}}$
We will see more details when we learn calculus
7. We denote the 'instantaneous angular velocity' by ω (the Greek letter omega)
• When we learned about circular motion, we saw that, the relation between this ω and the linear velocity 'v' is given by: v = rω
♦ Where r is the radius of the circle
8. Using this relation, we can find the instantaneous linear velocity of any particle in the rigid body
• For example, let there be n particles in the rigid body
• We can represent them as: 1st particle, 2nd particle, 3rd particle, . . . , nth particle
• For generality, consider the ith particle.
• We want it's linear velocity at the instant when the reading in the stop watch is 't'
• We can obtain it as: $\mathbf\small{v_{i(t)}=r_{\bot i} \times \omega_{(t)}}$
• Where:
♦ $\mathbf\small{\omega_{(t)}}$ is the instantaneous angular velocity of the rigid body, at the instant when the reading in the stop watch is 't'
♦ $\mathbf\small{r_{\bot i}}$ is the perpendicular distance of that ith particle from the axis
■ Why do we specifically write 'perpendicular distance'?
Answer can be written in 4 steps:
(i) Let the particle be at any random position that we select
(ii) From that position, there are 'infinite number of distances' possible to the axis
(iii) Some of those possible distances are indicated by the red lines in fig.7.77 below:
(iv) But there will be one and only one 'perpendicular distance'. This is indicated by the white line
• The white line is perpendicular to the axis
• It is the 'shortest possible distance' between the particle and the axis
• The white lines (of length $\mathbf\small{r_{\bot}}$) in the previous fig.7.76 are perpendicular distances
♦ One is the perpendicular distant at 'A'
♦ The other is the perpendicular distant at 'B'
9. For any particle situated on the axis of rotation, $\mathbf\small{r_{\bot}}$ = 0
• So the linear velocity of those particles = 0 × ω = 0
• That means, all particles on the axis are stationary
• This proves that the axis is fixed
10. For particles not on the axis, the $\mathbf\small{r_{\bot}}$ will be different for different particles
• So for all particles not on the axis, $\mathbf\small{\vec{v}}$ will be different for different particles
■ However, we must always remember that, ω is the same for all particles at any instant
11. Since the ω is the same for all the particles, we can say that, the 'rigid body as a whole' has a particular ω at any instant
■ We defined pure translation earlier:
All particles of the body will be having the same linear velocity at any instant
■ In a similar way, we can now define pure rotation:
All particles of the body will be having the same angular velocity ω at any instant
• If it is a vector, there will be both magnitude and direction
• We saw that the magnitude is given by: $\mathbf\small{\text{Instantaneous angular velocity}=\frac{d\theta}{dt}}$
• Now we want the direction
It can be explained by the following steps
1. Consider a rotating disc as shown in the fig.7.78(a) below:
• The direction of rotation is indicated by the orange curved arrow
• The blue line indicates the axis of rotation
2. Now, the $\mathbf\small{\vec{\omega}}$ will always lie along the axis of rotation
• So, in our present case, it will lie along the blue line
3. But we want more information:
• Is it from A to B?
• OR, Is it from B to A?
4. For that, we use the right hand screw rule
• It is applied as follows:
(i) Place a right handed screw along the axis of rotation
(ii) Turn the screw in the same direction in which the body is rotating
(Note that, in the fig.7.78(a) above, the brown curved arrow has the same direction as the orange curved arrow)
(iii) The ‘direction in which the screw moves’ gives the direction of omega vector
• The screw in fig.a will be moving towards the disc
• So the direction of $\mathbf\small{\vec{\omega}}$ in fig.a, is from A to B
• In fig.b, the disc is rotating in the opposite direction. So the brown curved arrow is also reversed
• The screw in this case will be moving away from the disc
• So in this case, the direction of $\mathbf\small{\vec{\omega}}$ is from B to A
1. In fig.7.79 below, a particle rotates about the z-axis
• So z-axis is the axis of rotation
• The direction of rotation is indicated by the yellow curved arrow
2. We know that, direction of $\mathbf\small{\vec{\omega}}$ of the particle will be along the axis of rotation
• So here it is along the z-axis
• Is $\mathbf\small{\vec{\omega}}$ directed towards the +ve side of z-axis ?
• OR, is it directed towards the -ve side of z-axis ?
3. To find the answer, we apply the right hand screw rule:
(i) The screw is shown at the bottom most portion, below the z-axis
(ii) We turn it in the same direction as the yellow curved arrow
(iii) Due to such a turning, the screw will move towards the +ve side of z-axis
(iv) So we write: $\mathbf\small{\vec{\omega}}$ of the particle is directed towards the +ve side of z-axis
• $\mathbf\small{\vec{\omega}}$ is indicated by the yellow vector at the top most point above the z-axis
4. In the fig.7.79, the position vector $\mathbf\small{\vec{r}}$ of the particle is also shown
• It is shown in brown color
• For defining a position vector, we need a frame of reference. Note that in this case, the origin 'O' of the frame of reference is placed on the axis of rotation
5. Let us take the cross product of $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{r}}$
We have: $\mathbf\small{\vec{\omega}\times \vec{r}=\vec{\omega}\times \vec{OP}}$
6. But $\mathbf\small{\vec{OP}}$ is the resultant of $\mathbf\small{\vec{OC}}$ and $\mathbf\small{\vec{CP}}$
That is: $\mathbf\small{\vec{OP}=(\vec{OC}+\vec{CP})}$
7. So the result in (5) becomes: $\mathbf\small{\vec{\omega}\times \vec{r}=\vec{\omega}\times (\vec{OC}+\vec{CP})}$
• We have seen that, cross products obey distributive property. So we can write:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times \vec{OC})+(\vec{\omega}\times\vec{CP})}$
8. Consider the first term on the right side: $\mathbf\small{(\vec{\omega}\times \vec{OC})}$
• $\mathbf\small{\vec{\omega}}$ lies along the z-axis
• $\mathbf\small{\vec{OC}}$ also lies along the z-axis
• So we get: $\mathbf\small{(\vec{\omega}\times \vec{OC})=|\vec{\omega}|\times |\vec{OC}| \times \sin 0=\vec{0}}$
9. Thus we need not consider the first term. The result in (7) becomes:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times\vec{CP})}$
10. Consider the vector multiplication on the right side
• The resulting vector from this multiplication should be perpendicular to both $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{CP}}$
• That is., the product vector must be perpendicular to the plane containing $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{CP}}$
• This plane is shown in cyan color in fig.7.80 below:
11. So the product vector that we are seeking, is perpendicular to the cyan plane. But we want more information:
• Is that vector directed towards us ?
• OR, Is it directed away from us?
• To find the answer, we apply the right hand screw rule:
(i) We place the screw perpendicular to the cyan plane
• This screw is shown in violet color
(ii) Now, in which direction do we turn that screw?
• To find the direction of $\mathbf\small{(\vec{\omega}\times \vec{CP})}$, we turn it in the direction from $\mathbf\small{\vec{\omega}}$ to $\mathbf\small{\vec{CP}}$
• To find the direction of $\mathbf\small{(\vec{CP}\times \vec{\omega})}$, we turn it in the direction from $\mathbf\small{\vec{CP}}$ to $\mathbf\small{\vec{\omega}}$
• So in our present case, we turn it from $\mathbf\small{\vec{\omega}}$ to $\mathbf\small{\vec{CP}}$
• This is indicated by the violet curved arrow
(Note that, to find the 'direction of turning', the two vectors must be placed such that, their tail ends coincide. In our present case, we see that, if we bring the $\mathbf\small{\vec{\omega}}$ downwards, the tail ends will coincide. Then the 'direction of turning' is indeed the one shown by the violet curved arrow)
(iii) When we turn it in the direction of the violet curved arrow, the screw will move away from us
• So we can write: The cross product $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to the cyan plane and is directed away from us
12. If $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to the cyan plane, it will be perpendicular to $\mathbf\small{\vec{CP}}$ also
• This is because, $\mathbf\small{\vec{CP}}$ lies in the cyan plane
■ If $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to $\mathbf\small{\vec{CP}}$, it will be tangential (at P) to the red circular path
• This is because, tangents are always perpendicular to the radius at the point of tangency
13. So now we have all the information about the direction of the 'cross product vector' that we are seeking
• The cross product $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ that we are seeking, is indicated by the magenta vector in fig.7.81 below:
14. Next we try to find the magnitude of that vector
We can write: $\mathbf\small{|(\vec{\omega}\times \vec{CP})|=|\vec{\omega}|\times r_{\bot}\times \sin 90=\omega \times r_{\bot}}$
15. Thus we can write the following 3 points:
(i) $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is the magenta vector shown in fig.7.81
(ii) It's direction is tangential (at P) to the red circular path
(iii) It's magnitude is $\mathbf\small{\omega \times r_{\bot}}$
16. Now consider the result in (9) that we saw earlier. We will write it again:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times\vec{CP})}$
17. Comparing (15) and (16), we can write the 3 points again:
(i) $\mathbf\small{(\vec{\omega}\times \vec{r})}$ is the magenta vector shown in fig.7.81
(ii) It's direction is tangential (at P) to the red circular path
(iii) It's magnitude is $\mathbf\small{\omega \times r_{\bot}}$
18. Now, based on the discussion that we had about circular motion in chapter 4 (Details here), we can write some details about our present particle in fig.7.81
• If at the instant when the particle is at P, the angular velocity is ω, then:
♦ The magnitude of the linear velocity $\mathbf\small{\vec{v}}$ at that instant is $\mathbf\small{\omega \times r_{\bot}}$
♦ The direction of the $\mathbf\small{\vec{v}}$ at that instant is tangential (at P) to the circular path
19. Comparing (17) and (18), we can write:
• The vector represented by $\mathbf\small{(\vec{\omega}\times \vec{r})}$, is none other than $\mathbf\small{\vec{v}}$
• That is:
Eq.7.16: $\mathbf\small{(\vec{\omega}\times \vec{r})=\vec{v}}$
■ This is a very useful result. From now on, we can calculate the tangential velocity of any particle in a rigid body. All we need to know are the following two items:
(i) Angular velocity vector $\mathbf\small{(\vec{\omega})}$ of the rigid body at that instant
(ii) The position vector $\mathbf\small{(\vec{r})}$ of that particle
• This is particularly helpful when the vectors are given in component forms. We do not need to find $\mathbf\small{r_{\bot}}$
20. If $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{r}}$ are given in component forms, we can find the cross product by writing the table or the determinant
• If they are not in component form, we will be given the magnitudes and the angle θ between them. This is shown in fig.7.81
• In that case we find the cross product as: $\mathbf\small{(\vec{\omega}\times \vec{r})=|\vec{\omega}|\times |\vec{r}|\times \sin \theta}$
• Note that, in the right triangle OPC in fig.7.81, $\mathbf\small{|\vec{r}|\times \sin \theta=r_{\bot}}$
From our discussion so far, it is clear that, translational motion and rotational motion are analogous. We can write the following points:
1. In translational motion, we have linear displacement x
• In rotational motion, we have angular displacement θ
2. In translational motion, we have linear velocity v
♦ It is given by: $\mathbf\small{v = \frac{\text{displacement}}{time}=\frac{dx}{dt}}$
• In rotational motion, we have angular velocity ω
♦ It is given by: $\mathbf\small{\omega = \frac{\text{angular displacement}}{time}=\frac{d\theta}{dt}}$
3. In the same way, we can write about acceleration also:
• In translational motion, we have linear acceleration a
♦ It is given by: $\mathbf\small{a = \frac{\text{change in linear velocity}}{time}=\frac{dv}{dt}}$
• In rotational motion, we have angular acceleration
♦ It is denoted as α
♦ It is given by: $\mathbf\small{\alpha = \frac{\text{change in angular velocity}}{time}=\frac{d\omega}{dt}}$
We have seen the characteristics of rotational motion in a previous section of this chapter (Details here)
There we saw this:
■ If a rigid body is in rotation about a fixed axis, then 3 facts can be written:
2. Each of the other particles will be rotating in it's own circular path
♦ The center of that circular path lies on the axis
♦ Radius of that circular path = Perpendicular distance of the particle from the axis
3. That circular path lies on a plane
♦ This plane is perpendicular to the axis
Now we will write the steps to find angular velocity:
1. Consider a rigid body in rotation about a fixed axis. Let us isolate a 'single particle' in that rigid body
1. Consider a rigid body in rotation about a fixed axis. Let us isolate a 'single particle' in that rigid body
 |
| Fig.7.76 |
2. At the instant when the reading in the stop watch is 't1', the particle is at A
♦ The linear velocity of the particle at that instant is $\mathbf\small{\vec{v}_{(t1)}}$
♦ It is tangential to the circular path
♦ It is shown in magenta color
• At the instant when the reading in the stop watch is 't2', the particle is at B
♦ The linear velocity of the particle at that instant is $\mathbf\small{\vec{v}_{(t2)}}$
♦ It is tangential to the circular path
♦ It is shown in magenta color
3. The time elapsed between the two instants = Δt = (t2-t1)
• During this time interval Δt, the particle turns through ∠AOB
• We will denote this ∠AOB as Δθ.
4. We know that $\mathbf\small{\text{Linear velocity}=\frac{\text{Displacement}}{time}}$
• In a similar way, $\mathbf\small{\text{Angular velocity}=\frac{\text{Angular displacement}}{time}}$
• So we can write:
The angular velocity with which the particle travels from A to B = $\mathbf\small{\frac{\Delta \theta}{\Delta t}}$
5. But the rotation may not be uniform. That is., angular velocity may be different at different instances
• In such a situation, the the result obtained in (4) will be the 'average angular velocity'
6. If we make the time interval Δt smaller and smaller, it will tend to become zero
• If Δt is very close to zero, we can call it an instant
• Then the result obtained in (4) will be the 'instantaneous angular velocity'
(Note that, Δt must not become exact zero. Then we do not have an instant. Besides, division by zero is undefined)
• The evaluation of 'instantaneous angular velocity' when Δt is very small, can be easily done using calculus
The formula is: $\mathbf\small{\text{Instantaneous angular velocity}=\frac{d\theta}{dt}}$
We will see more details when we learn calculus
7. We denote the 'instantaneous angular velocity' by ω (the Greek letter omega)
• When we learned about circular motion, we saw that, the relation between this ω and the linear velocity 'v' is given by: v = rω
♦ Where r is the radius of the circle
8. Using this relation, we can find the instantaneous linear velocity of any particle in the rigid body
• For example, let there be n particles in the rigid body
• We can represent them as: 1st particle, 2nd particle, 3rd particle, . . . , nth particle
• For generality, consider the ith particle.
• We want it's linear velocity at the instant when the reading in the stop watch is 't'
• We can obtain it as: $\mathbf\small{v_{i(t)}=r_{\bot i} \times \omega_{(t)}}$
• Where:
♦ $\mathbf\small{\omega_{(t)}}$ is the instantaneous angular velocity of the rigid body, at the instant when the reading in the stop watch is 't'
♦ $\mathbf\small{r_{\bot i}}$ is the perpendicular distance of that ith particle from the axis
■ Why do we specifically write 'perpendicular distance'?
Answer can be written in 4 steps:
(i) Let the particle be at any random position that we select
(ii) From that position, there are 'infinite number of distances' possible to the axis
(iii) Some of those possible distances are indicated by the red lines in fig.7.77 below:
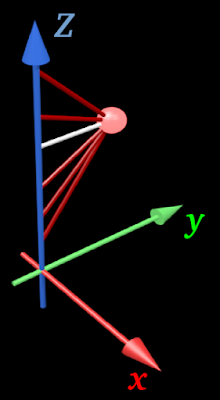 |
| Fig.7.77 |
• The white line is perpendicular to the axis
• It is the 'shortest possible distance' between the particle and the axis
• The white lines (of length $\mathbf\small{r_{\bot}}$) in the previous fig.7.76 are perpendicular distances
♦ One is the perpendicular distant at 'A'
♦ The other is the perpendicular distant at 'B'
9. For any particle situated on the axis of rotation, $\mathbf\small{r_{\bot}}$ = 0
• So the linear velocity of those particles = 0 × ω = 0
• That means, all particles on the axis are stationary
• This proves that the axis is fixed
10. For particles not on the axis, the $\mathbf\small{r_{\bot}}$ will be different for different particles
• So for all particles not on the axis, $\mathbf\small{\vec{v}}$ will be different for different particles
■ However, we must always remember that, ω is the same for all particles at any instant
11. Since the ω is the same for all the particles, we can say that, the 'rigid body as a whole' has a particular ω at any instant
■ We defined pure translation earlier:
All particles of the body will be having the same linear velocity at any instant
■ In a similar way, we can now define pure rotation:
All particles of the body will be having the same angular velocity ω at any instant
• From the above discussion, we get the impression that, the angular velocity is a scalar. But in fact, it is a vector. We will see the proof in higher classes.
• We saw that the magnitude is given by: $\mathbf\small{\text{Instantaneous angular velocity}=\frac{d\theta}{dt}}$
• Now we want the direction
It can be explained by the following steps
1. Consider a rotating disc as shown in the fig.7.78(a) below:
 |
| Fig.7.78 |
• The blue line indicates the axis of rotation
2. Now, the $\mathbf\small{\vec{\omega}}$ will always lie along the axis of rotation
• So, in our present case, it will lie along the blue line
3. But we want more information:
• Is it from A to B?
• OR, Is it from B to A?
4. For that, we use the right hand screw rule
• It is applied as follows:
(i) Place a right handed screw along the axis of rotation
(ii) Turn the screw in the same direction in which the body is rotating
(Note that, in the fig.7.78(a) above, the brown curved arrow has the same direction as the orange curved arrow)
(iii) The ‘direction in which the screw moves’ gives the direction of omega vector
• The screw in fig.a will be moving towards the disc
• So the direction of $\mathbf\small{\vec{\omega}}$ in fig.a, is from A to B
• In fig.b, the disc is rotating in the opposite direction. So the brown curved arrow is also reversed
• The screw in this case will be moving away from the disc
• So in this case, the direction of $\mathbf\small{\vec{\omega}}$ is from B to A
Now we will find the relation between linear and angular velocities of the particle:
• So z-axis is the axis of rotation
 |
| Fig.7.79 |
• The direction of rotation is indicated by the yellow curved arrow
2. We know that, direction of $\mathbf\small{\vec{\omega}}$ of the particle will be along the axis of rotation
• So here it is along the z-axis
• Is $\mathbf\small{\vec{\omega}}$ directed towards the +ve side of z-axis ?
• OR, is it directed towards the -ve side of z-axis ?
3. To find the answer, we apply the right hand screw rule:
(i) The screw is shown at the bottom most portion, below the z-axis
(ii) We turn it in the same direction as the yellow curved arrow
(iii) Due to such a turning, the screw will move towards the +ve side of z-axis
(iv) So we write: $\mathbf\small{\vec{\omega}}$ of the particle is directed towards the +ve side of z-axis
• $\mathbf\small{\vec{\omega}}$ is indicated by the yellow vector at the top most point above the z-axis
4. In the fig.7.79, the position vector $\mathbf\small{\vec{r}}$ of the particle is also shown
• It is shown in brown color
• For defining a position vector, we need a frame of reference. Note that in this case, the origin 'O' of the frame of reference is placed on the axis of rotation
5. Let us take the cross product of $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{r}}$
We have: $\mathbf\small{\vec{\omega}\times \vec{r}=\vec{\omega}\times \vec{OP}}$
6. But $\mathbf\small{\vec{OP}}$ is the resultant of $\mathbf\small{\vec{OC}}$ and $\mathbf\small{\vec{CP}}$
That is: $\mathbf\small{\vec{OP}=(\vec{OC}+\vec{CP})}$
7. So the result in (5) becomes: $\mathbf\small{\vec{\omega}\times \vec{r}=\vec{\omega}\times (\vec{OC}+\vec{CP})}$
• We have seen that, cross products obey distributive property. So we can write:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times \vec{OC})+(\vec{\omega}\times\vec{CP})}$
8. Consider the first term on the right side: $\mathbf\small{(\vec{\omega}\times \vec{OC})}$
• $\mathbf\small{\vec{\omega}}$ lies along the z-axis
• $\mathbf\small{\vec{OC}}$ also lies along the z-axis
• So we get: $\mathbf\small{(\vec{\omega}\times \vec{OC})=|\vec{\omega}|\times |\vec{OC}| \times \sin 0=\vec{0}}$
9. Thus we need not consider the first term. The result in (7) becomes:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times\vec{CP})}$
10. Consider the vector multiplication on the right side
• The resulting vector from this multiplication should be perpendicular to both $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{CP}}$
• That is., the product vector must be perpendicular to the plane containing $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{CP}}$
• This plane is shown in cyan color in fig.7.80 below:
 |
| Fig.7.80 |
11. So the product vector that we are seeking, is perpendicular to the cyan plane. But we want more information:
• Is that vector directed towards us ?
• OR, Is it directed away from us?
• To find the answer, we apply the right hand screw rule:
(i) We place the screw perpendicular to the cyan plane
• This screw is shown in violet color
(ii) Now, in which direction do we turn that screw?
• To find the direction of $\mathbf\small{(\vec{\omega}\times \vec{CP})}$, we turn it in the direction from $\mathbf\small{\vec{\omega}}$ to $\mathbf\small{\vec{CP}}$
• To find the direction of $\mathbf\small{(\vec{CP}\times \vec{\omega})}$, we turn it in the direction from $\mathbf\small{\vec{CP}}$ to $\mathbf\small{\vec{\omega}}$
• So in our present case, we turn it from $\mathbf\small{\vec{\omega}}$ to $\mathbf\small{\vec{CP}}$
• This is indicated by the violet curved arrow
(Note that, to find the 'direction of turning', the two vectors must be placed such that, their tail ends coincide. In our present case, we see that, if we bring the $\mathbf\small{\vec{\omega}}$ downwards, the tail ends will coincide. Then the 'direction of turning' is indeed the one shown by the violet curved arrow)
(iii) When we turn it in the direction of the violet curved arrow, the screw will move away from us
• So we can write: The cross product $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to the cyan plane and is directed away from us
12. If $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to the cyan plane, it will be perpendicular to $\mathbf\small{\vec{CP}}$ also
• This is because, $\mathbf\small{\vec{CP}}$ lies in the cyan plane
■ If $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is perpendicular to $\mathbf\small{\vec{CP}}$, it will be tangential (at P) to the red circular path
• This is because, tangents are always perpendicular to the radius at the point of tangency
13. So now we have all the information about the direction of the 'cross product vector' that we are seeking
• The cross product $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ that we are seeking, is indicated by the magenta vector in fig.7.81 below:
 |
| Fig.7.81 |
14. Next we try to find the magnitude of that vector
We can write: $\mathbf\small{|(\vec{\omega}\times \vec{CP})|=|\vec{\omega}|\times r_{\bot}\times \sin 90=\omega \times r_{\bot}}$
15. Thus we can write the following 3 points:
(i) $\mathbf\small{(\vec{\omega}\times \vec{CP})}$ is the magenta vector shown in fig.7.81
(ii) It's direction is tangential (at P) to the red circular path
(iii) It's magnitude is $\mathbf\small{\omega \times r_{\bot}}$
16. Now consider the result in (9) that we saw earlier. We will write it again:
$\mathbf\small{\vec{\omega}\times \vec{r}=(\vec{\omega}\times\vec{CP})}$
17. Comparing (15) and (16), we can write the 3 points again:
(i) $\mathbf\small{(\vec{\omega}\times \vec{r})}$ is the magenta vector shown in fig.7.81
(ii) It's direction is tangential (at P) to the red circular path
(iii) It's magnitude is $\mathbf\small{\omega \times r_{\bot}}$
18. Now, based on the discussion that we had about circular motion in chapter 4 (Details here), we can write some details about our present particle in fig.7.81
• If at the instant when the particle is at P, the angular velocity is ω, then:
♦ The magnitude of the linear velocity $\mathbf\small{\vec{v}}$ at that instant is $\mathbf\small{\omega \times r_{\bot}}$
♦ The direction of the $\mathbf\small{\vec{v}}$ at that instant is tangential (at P) to the circular path
19. Comparing (17) and (18), we can write:
• The vector represented by $\mathbf\small{(\vec{\omega}\times \vec{r})}$, is none other than $\mathbf\small{\vec{v}}$
• That is:
Eq.7.16: $\mathbf\small{(\vec{\omega}\times \vec{r})=\vec{v}}$
■ This is a very useful result. From now on, we can calculate the tangential velocity of any particle in a rigid body. All we need to know are the following two items:
(i) Angular velocity vector $\mathbf\small{(\vec{\omega})}$ of the rigid body at that instant
(ii) The position vector $\mathbf\small{(\vec{r})}$ of that particle
• This is particularly helpful when the vectors are given in component forms. We do not need to find $\mathbf\small{r_{\bot}}$
20. If $\mathbf\small{\vec{\omega}}$ and $\mathbf\small{\vec{r}}$ are given in component forms, we can find the cross product by writing the table or the determinant
• If they are not in component form, we will be given the magnitudes and the angle θ between them. This is shown in fig.7.81
• In that case we find the cross product as: $\mathbf\small{(\vec{\omega}\times \vec{r})=|\vec{\omega}|\times |\vec{r}|\times \sin \theta}$
• Note that, in the right triangle OPC in fig.7.81, $\mathbf\small{|\vec{r}|\times \sin \theta=r_{\bot}}$
Angular acceleration
1. In translational motion, we have linear displacement x
• In rotational motion, we have angular displacement θ
2. In translational motion, we have linear velocity v
♦ It is given by: $\mathbf\small{v = \frac{\text{displacement}}{time}=\frac{dx}{dt}}$
• In rotational motion, we have angular velocity ω
♦ It is given by: $\mathbf\small{\omega = \frac{\text{angular displacement}}{time}=\frac{d\theta}{dt}}$
3. In the same way, we can write about acceleration also:
• In translational motion, we have linear acceleration a
♦ It is given by: $\mathbf\small{a = \frac{\text{change in linear velocity}}{time}=\frac{dv}{dt}}$
• In rotational motion, we have angular acceleration
♦ It is denoted as α
♦ It is given by: $\mathbf\small{\alpha = \frac{\text{change in angular velocity}}{time}=\frac{d\omega}{dt}}$
In the next section, we will see torque
No comments:
Post a Comment