In the previous section, we completed a discussion on torque and center of gravity. We saw some solved examples also. In this section we will see moment of inertia
In our discussions so far, we saw these:
• An important role is played by 'force’ in translational motion
♦ In rotational motion, that role is played by ‘moment of force’ or 'torque' ($\mathbf\small{\vec{\tau}}$)
• An important role is played by 'linear momentum’ in translational motion
♦ In rotational motion, that role is played by 'angular momentum' ($\mathbf\small{\vec{l}}$)
♦ Angular momentum can be considered as the ‘moment of linear momentum’
• Moment of a force is given by: $\mathbf\small{\vec{\tau}=\vec{r}\times \vec{F}}$
♦ In a similar way, moment of linear momentum ($\mathbf\small{\vec{p}}$) is given by: $\mathbf\small{\vec{l}=\vec{r}\times \vec{p}}$
■ We know that, 'mass' plays an important role in translational motion
• So next, we want to see who plays the role of 'mass' in rotational motion
1. Consider a body rotating about a fixed axis
• Consider any one particle in that body
• In a previous section, we have seen Eq.7.16 which gives the linear velocity of 'a particle in a rotating body' (Details here)
• Eq.7.16: $\mathbf\small{\vec{v}=\vec{r}\times \vec{\omega}}$
• So we can write:
Linear velocity (vi) of the ith particle at any instant is given by: $\mathbf\small{\vec{v}_i=\vec{r}_i\times \vec{\omega}}$
• Where:
♦ $\mathbf\small{\vec{r}_i}$ is the position vector of that particle
(with origin 'O' on the axis of rotation)
♦ $\mathbf\small{\vec{\omega}}$ is the angular velocity of the whole body at that instant
2. This is a vector cross product. The result will be the velocity vector
• We want the magnitude of that resulting velocity vector. This is because, kinetic energy is calculated using the 'magnitude of velocity'
3. We have: $\mathbf\small{|\vec{v}_i|=|\vec{r}_i|\times |\vec{\omega}| \times \sin \theta}$
• This can be rearranged as:
$\mathbf\small{|\vec{v}_i|=\left(|\vec{r}_i|\times \sin \theta \right)\times |\vec{\omega}|}$
$\mathbf\small{\Rightarrow |\vec{v}_i|=r_{i(\bot)}\times |\vec{\omega}|}$
• Where $\mathbf\small{r_{i(\bot)}}$ is the perpendicular distance of that particle from the axis of rotation
4. Once we get the above magnitude, we can calculate the kinetic energy possessed by that particle at that instant
• We have the familiar equation:
Kinetic energy (K) = $\mathbf\small{\frac{1}{2}m|\vec{v}|^2}$
• So, for the ith particle, we have: $\mathbf\small{K_i=\frac{1}{2}m_i|\vec{v}_i|^2}$
• Substituting for vi from (3), we get:
$\mathbf\small{K_i=\frac{1}{2}m_i\left(r_{i(\bot)}\;|\vec{\omega}|\right)^2}$
$\mathbf\small{\Rightarrow K_i=\frac{1}{2}m_i\;r_{i(\bot)}^2\;|\vec{\omega}|^2}$
5. So we obtained the kinetic energy of one particle of the body
• If we add the kinetic energies of all the particles, we will get the 'kinetic energy possessed by the whole body'
• Thus we get: $\mathbf\small{K=\sum\limits_{i=1}^{i=n}{K_i} }$
$\mathbf\small{\Rightarrow K=\sum\limits_{i=1}^{i=n}{\left(\frac{1}{2}m_i\;r_{i(\bot)}^2\;|\vec{\omega}|^2 \right)} }$
6. $\mathbf\small{\frac{1}{2}}$ and $\mathbf\small{|\vec{\omega}|^2}$ are same for all the particles. So they can be taken outside the summation
• Thus we get:
$\mathbf\small{K=\frac{1}{2}\;|\vec{\omega}|^2\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
7. In the above result, consider the quantity inside the brackets: $\mathbf\small{m_i\;r_{i(\bot)}^2}$
• We can elaborate it as follows:
Take any particle in the rigid body. Note down three items related to that particle:
(i) It's mass. Let it be $\mathbf\small{m_i}$
(ii) It's perpendicular distance from the axis. Let it be $\mathbf\small{r_{i(\bot)}}$
(iii) Calculate $\mathbf\small{m_i\;r_{i(\bot)}^2}$ for that particle
• In this way calculate $\mathbf\small{m_i\;r_{i(\bot)}^2}$ for all the n particles
• Then take their sum: $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
■ This sum has much significance. It is given a special name: Moment of inertia. It's symbol is: I
• So we can write:
Eq.7.25: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
8. Let us see the important features of I:
(i) We see that, for calculating I, we do not require $\mathbf\small{\vec{\omega}}$
• That means, what ever be the angular velocity of the body. The I of that body will not change
(ii) We know that 'masses of the particles' will not change
• Also the 'perpendicular distances of the particles from the axis' will not change
■ So I of a body is a unique value
■ In other words, every rigid body has it's own unique I
9. Is there any situation in which the I of a body changes?
■ There are indeed such situations. Let us analyse it:
• We know that, 'perpendicular distances of the particles from the axis' will not change
• But if the 'axis' is changed, then those 'perpendicular distances' will change
• Consequently, the I will change
10. So we will modify the final statement that we wrote in (8) above
• We can write it in 3 steps:
(i) A rigid body can have infinite number of lines as it's 'axis of rotation'
(ii) That rigid body may rotate about any one of those possible axes
(iii) That rigid body will have a unique I for each of those axes
• Another way of writing it in 3 steps:
(i) A rigid body can have infinite number of lines as it's 'axis of rotation'
(ii) Select any one axis from among them
(iii) That rigid body will have a unique I with respect to that selected axis
■ It is given the status 'unique' because, once the axis is selected, the I will not change unless the shape of the body itself changes
11. Now that we have decided to represent $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$ by I, the result in (6) becomes :
Eq.7.26: $\mathbf\small{K=\frac{1}{2}\;I\;|\vec{\omega}|^2}$
• This equation gives us the kinetic energy of a body in pure rotation
12. We know that, the kinetic energy of a body in pure translation is given by:
$\mathbf\small{K=\frac{1}{2}\;m\;|\vec{v}|^2}$
13. Let us compare (11) and (12):
• We already know that $\mathbf\small{\vec{\omega}}$ in rotational motion is analogous to $\mathbf\small{\vec{v}}$ in translational motion
■ So we can write:
• 'Mass' plays an important role in translational motion
• In rotational motion, that role is played by 'moment of inertia (I)'
• Let us now calculate the I of a thin circular ring. We will write it in steps:
1. We know that, the I depends on the axis of rotation
• In our present case:
♦ The ring is rotating on it’s own plane
♦ Also, it is rotating about it’s center
• So it is clear that:
♦ The axis is perpendicular to the ring
♦ Also, the axis passes through the center of the ring
• This is shown in the animation in fig.7.108 below:
• The magenta line is the axis of rotation
2. In fig.7.109 below, a particle in the ring is isolated for analysis
• It is shown as a red sphere
• A point on the axis is chosen as the origin 'O'
• The position vector of the particle is $\mathbf\small{\vec{r}}$
• The perpendicular distance of the particle from the axis is $\mathbf\small{r_{\bot}}$
• The direction of rotation is indicated by the blue curved arrow
3. Let there be n particles in the ring
• Each of them will have it's own position vector
• But all those position vectors will be having the same magnitude $\mathbf\small{|\vec{r}|}$
• And all of them will be making the same angle θ with the axis
• So the perpendicular distance ($\mathbf\small{r_{\bot}}$) of the particle (given by $\mathbf\small{|\vec{r}|\sin \theta}$) will be same for all particles
4. We want to find I
• We have: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• Since the perpendicular distances are the same, it can be taken outside the brackets. So we get:
$\mathbf\small{I=r_{\bot}^2\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$
5. But $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$ is the total mass M of the ring
• Also, $\mathbf\small{r_{\bot}}$ is the radius R of the ring
6. So the result in (4) becomes: I = MR2.
• This is the moment of inertia of a thin ring, about the 'perpendicular axis passing through it's center'
• In this example, we used the position vector in the analysis
♦ This is for obtaining a basic understanding only
♦ What we actually need is the perpendicular distances $\mathbf\small{r_{i(\bot)}}$
1. Take a rigid massless rod of length l.
• Attach two equal masses at the ends. Let each mass be $\mathbf\small{\frac{M}{2}}$
• The axis of rotation passes through the center of the rod
• Also, the axis is perpendicular to the rod
• This is shown in the animation in fig.7.110 below:
• The magenta line is the axis of rotation
2. We want to find I
We have: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• The distances are shown in fig.7.111 below:
• Since the perpendicular distances are the same, it can be taken outside the brackets. So we get:
$\mathbf\small{I=r_{\bot}^2\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$
3. But $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$ is the total mass of the system
• This is equal to $\mathbf\small{\frac{M}{2}+\frac{M}{2}=M}$
• Also, $\mathbf\small{r_{\bot}=\frac{l}{2}}$
4. So the result in (2) becomes: $\mathbf\small{I=M\left(\frac{l}{2} \right)^2=\frac{Ml^2}{4}}$
1. Body: Thin circular ring of radius R
Axis: Perpendicular to the plane of the ring, passing through the center
• We already saw this case. We obtained $\mathbf\small{I=MR^2}$
2. Body: Thin circular ring of radius R
Axis: Lies on the plane of the ring, passing through the center. Obviously, this axis is the extension of any one diameter of the ring
• This is shown in fig.7.112(a) below:
■ In this case, $\mathbf\small{I=\frac{MR^2}{2}}$
3. Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
• This is shown in fig.7.112(b) above
■ In this case, $\mathbf\small{I=\frac{ML^2}{12}}$
4. Body: Circular disc of radius R
Axis: Perpendicular to the disc, passing through the center
• This is shown in fig.7.113(a) below
■ In this case, $\mathbf\small{I=\frac{MR^2}{2}}$
5. Body: Circular disc of radius R
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
• This is shown in fig.7.113(b) above
■ In this case, $\mathbf\small{I=\frac{MR^2}{4}}$
6. Body: Solid cylinder of radius R
Axis: Axis of the cylinder
• This is shown in fig.7.114(a) below
■ In this case, $\mathbf\small{I=\frac{MR^2}{2}}$
7. Body: Hollow cylinder of radius R
Axis: Axis of the cylinder
• This is shown in fig.7.114(b) above
■ In this case, $\mathbf\small{I=MR^2}$
8. Body: Solid sphere of radius R
Axis: Passes through the center. Obviously, this axis is the extension of any one diameter of the sphere
• This is shown in fig.7.115 below:
■ In this case, $\mathbf\small{I=\frac{2MR^2}{5}}$
In our discussions so far, we saw these:
• An important role is played by 'force’ in translational motion
♦ In rotational motion, that role is played by ‘moment of force’ or 'torque' ($\mathbf\small{\vec{\tau}}$)
• An important role is played by 'linear momentum’ in translational motion
♦ In rotational motion, that role is played by 'angular momentum' ($\mathbf\small{\vec{l}}$)
♦ Angular momentum can be considered as the ‘moment of linear momentum’
• Moment of a force is given by: $\mathbf\small{\vec{\tau}=\vec{r}\times \vec{F}}$
♦ In a similar way, moment of linear momentum ($\mathbf\small{\vec{p}}$) is given by: $\mathbf\small{\vec{l}=\vec{r}\times \vec{p}}$
■ We know that, 'mass' plays an important role in translational motion
• So next, we want to see who plays the role of 'mass' in rotational motion
• Consider any one particle in that body
• In a previous section, we have seen Eq.7.16 which gives the linear velocity of 'a particle in a rotating body' (Details here)
• Eq.7.16: $\mathbf\small{\vec{v}=\vec{r}\times \vec{\omega}}$
• So we can write:
Linear velocity (vi) of the ith particle at any instant is given by: $\mathbf\small{\vec{v}_i=\vec{r}_i\times \vec{\omega}}$
• Where:
♦ $\mathbf\small{\vec{r}_i}$ is the position vector of that particle
(with origin 'O' on the axis of rotation)
♦ $\mathbf\small{\vec{\omega}}$ is the angular velocity of the whole body at that instant
2. This is a vector cross product. The result will be the velocity vector
• We want the magnitude of that resulting velocity vector. This is because, kinetic energy is calculated using the 'magnitude of velocity'
3. We have: $\mathbf\small{|\vec{v}_i|=|\vec{r}_i|\times |\vec{\omega}| \times \sin \theta}$
• This can be rearranged as:
$\mathbf\small{|\vec{v}_i|=\left(|\vec{r}_i|\times \sin \theta \right)\times |\vec{\omega}|}$
$\mathbf\small{\Rightarrow |\vec{v}_i|=r_{i(\bot)}\times |\vec{\omega}|}$
• Where $\mathbf\small{r_{i(\bot)}}$ is the perpendicular distance of that particle from the axis of rotation
4. Once we get the above magnitude, we can calculate the kinetic energy possessed by that particle at that instant
• We have the familiar equation:
Kinetic energy (K) = $\mathbf\small{\frac{1}{2}m|\vec{v}|^2}$
• So, for the ith particle, we have: $\mathbf\small{K_i=\frac{1}{2}m_i|\vec{v}_i|^2}$
• Substituting for vi from (3), we get:
$\mathbf\small{K_i=\frac{1}{2}m_i\left(r_{i(\bot)}\;|\vec{\omega}|\right)^2}$
$\mathbf\small{\Rightarrow K_i=\frac{1}{2}m_i\;r_{i(\bot)}^2\;|\vec{\omega}|^2}$
5. So we obtained the kinetic energy of one particle of the body
• If we add the kinetic energies of all the particles, we will get the 'kinetic energy possessed by the whole body'
• Thus we get: $\mathbf\small{K=\sum\limits_{i=1}^{i=n}{K_i} }$
$\mathbf\small{\Rightarrow K=\sum\limits_{i=1}^{i=n}{\left(\frac{1}{2}m_i\;r_{i(\bot)}^2\;|\vec{\omega}|^2 \right)} }$
6. $\mathbf\small{\frac{1}{2}}$ and $\mathbf\small{|\vec{\omega}|^2}$ are same for all the particles. So they can be taken outside the summation
• Thus we get:
$\mathbf\small{K=\frac{1}{2}\;|\vec{\omega}|^2\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
7. In the above result, consider the quantity inside the brackets: $\mathbf\small{m_i\;r_{i(\bot)}^2}$
• We can elaborate it as follows:
Take any particle in the rigid body. Note down three items related to that particle:
(i) It's mass. Let it be $\mathbf\small{m_i}$
(ii) It's perpendicular distance from the axis. Let it be $\mathbf\small{r_{i(\bot)}}$
(iii) Calculate $\mathbf\small{m_i\;r_{i(\bot)}^2}$ for that particle
• In this way calculate $\mathbf\small{m_i\;r_{i(\bot)}^2}$ for all the n particles
• Then take their sum: $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
■ This sum has much significance. It is given a special name: Moment of inertia. It's symbol is: I
• So we can write:
Eq.7.25: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
8. Let us see the important features of I:
(i) We see that, for calculating I, we do not require $\mathbf\small{\vec{\omega}}$
• That means, what ever be the angular velocity of the body. The I of that body will not change
(ii) We know that 'masses of the particles' will not change
• Also the 'perpendicular distances of the particles from the axis' will not change
■ So I of a body is a unique value
■ In other words, every rigid body has it's own unique I
9. Is there any situation in which the I of a body changes?
■ There are indeed such situations. Let us analyse it:
• We know that, 'perpendicular distances of the particles from the axis' will not change
• But if the 'axis' is changed, then those 'perpendicular distances' will change
• Consequently, the I will change
10. So we will modify the final statement that we wrote in (8) above
• We can write it in 3 steps:
(i) A rigid body can have infinite number of lines as it's 'axis of rotation'
(ii) That rigid body may rotate about any one of those possible axes
(iii) That rigid body will have a unique I for each of those axes
• Another way of writing it in 3 steps:
(i) A rigid body can have infinite number of lines as it's 'axis of rotation'
(ii) Select any one axis from among them
(iii) That rigid body will have a unique I with respect to that selected axis
■ It is given the status 'unique' because, once the axis is selected, the I will not change unless the shape of the body itself changes
11. Now that we have decided to represent $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$ by I, the result in (6) becomes :
Eq.7.26: $\mathbf\small{K=\frac{1}{2}\;I\;|\vec{\omega}|^2}$
• This equation gives us the kinetic energy of a body in pure rotation
12. We know that, the kinetic energy of a body in pure translation is given by:
$\mathbf\small{K=\frac{1}{2}\;m\;|\vec{v}|^2}$
13. Let us compare (11) and (12):
• We already know that $\mathbf\small{\vec{\omega}}$ in rotational motion is analogous to $\mathbf\small{\vec{v}}$ in translational motion
■ So we can write:
• 'Mass' plays an important role in translational motion
• In rotational motion, that role is played by 'moment of inertia (I)'
• Moment of inertia (I) is an important parameter. It is essential that, we know it’s value for commonly occurring bodies like rectangles, rings, cylinders, spheres, etc.,
1. We know that, the I depends on the axis of rotation
• In our present case:
♦ The ring is rotating on it’s own plane
♦ Also, it is rotating about it’s center
• So it is clear that:
♦ The axis is perpendicular to the ring
♦ Also, the axis passes through the center of the ring
• This is shown in the animation in fig.7.108 below:
 |
| Fig.7.108 |
2. In fig.7.109 below, a particle in the ring is isolated for analysis
 |
| Fig.7.109 |
• A point on the axis is chosen as the origin 'O'
• The position vector of the particle is $\mathbf\small{\vec{r}}$
• The perpendicular distance of the particle from the axis is $\mathbf\small{r_{\bot}}$
• The direction of rotation is indicated by the blue curved arrow
3. Let there be n particles in the ring
• Each of them will have it's own position vector
• But all those position vectors will be having the same magnitude $\mathbf\small{|\vec{r}|}$
• And all of them will be making the same angle θ with the axis
• So the perpendicular distance ($\mathbf\small{r_{\bot}}$) of the particle (given by $\mathbf\small{|\vec{r}|\sin \theta}$) will be same for all particles
4. We want to find I
• We have: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• Since the perpendicular distances are the same, it can be taken outside the brackets. So we get:
$\mathbf\small{I=r_{\bot}^2\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$
5. But $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$ is the total mass M of the ring
• Also, $\mathbf\small{r_{\bot}}$ is the radius R of the ring
6. So the result in (4) becomes: I = MR2.
• This is the moment of inertia of a thin ring, about the 'perpendicular axis passing through it's center'
• In this example, we used the position vector in the analysis
♦ This is for obtaining a basic understanding only
♦ What we actually need is the perpendicular distances $\mathbf\small{r_{i(\bot)}}$
Another example:
• Attach two equal masses at the ends. Let each mass be $\mathbf\small{\frac{M}{2}}$
• The axis of rotation passes through the center of the rod
• Also, the axis is perpendicular to the rod
• This is shown in the animation in fig.7.110 below:
 |
| Fig.7.110 |
2. We want to find I
We have: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• The distances are shown in fig.7.111 below:
 |
| Fig.7.111 |
$\mathbf\small{I=r_{\bot}^2\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$
3. But $\mathbf\small{\sum\limits_{i=1}^{i=n}{\left(m_i \right)}}$ is the total mass of the system
• This is equal to $\mathbf\small{\frac{M}{2}+\frac{M}{2}=M}$
• Also, $\mathbf\small{r_{\bot}=\frac{l}{2}}$
4. So the result in (2) becomes: $\mathbf\small{I=M\left(\frac{l}{2} \right)^2=\frac{Ml^2}{4}}$
Thus we saw the I of two simple systems. For more complex bodies and systems, we can find I with the help of calculus. The I of some common bodies are given below:
1. Body: Thin circular ring of radius R
Axis: Perpendicular to the plane of the ring, passing through the center
• We already saw this case. We obtained $\mathbf\small{I=MR^2}$
2. Body: Thin circular ring of radius R
Axis: Lies on the plane of the ring, passing through the center. Obviously, this axis is the extension of any one diameter of the ring
• This is shown in fig.7.112(a) below:
 |
| Fig.7.112 |
3. Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
• This is shown in fig.7.112(b) above
■ In this case, $\mathbf\small{I=\frac{ML^2}{12}}$
4. Body: Circular disc of radius R
Axis: Perpendicular to the disc, passing through the center
• This is shown in fig.7.113(a) below
■ In this case, $\mathbf\small{I=\frac{MR^2}{2}}$
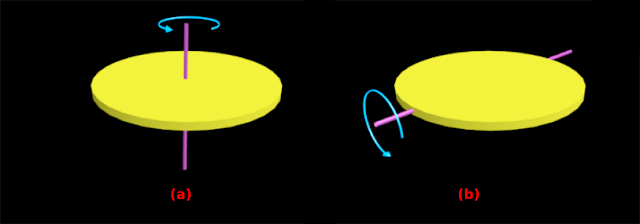 |
| Fig.7.113 |
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
• This is shown in fig.7.113(b) above
■ In this case, $\mathbf\small{I=\frac{MR^2}{4}}$
6. Body: Solid cylinder of radius R
Axis: Axis of the cylinder
• This is shown in fig.7.114(a) below
■ In this case, $\mathbf\small{I=\frac{MR^2}{2}}$
 |
| Fig.7.114 |
Axis: Axis of the cylinder
• This is shown in fig.7.114(b) above
■ In this case, $\mathbf\small{I=MR^2}$
8. Body: Solid sphere of radius R
Axis: Passes through the center. Obviously, this axis is the extension of any one diameter of the sphere
• This is shown in fig.7.115 below:
 |
| Fig.7.115 |
In the next section, we will see radius of gyration
No comments:
Post a Comment