Chapter 7.1 - Rotation About An Axis

In the previous section, we saw that, motion of a rigid body can be: [Translation + 'something else']. In this section, we will see what this 'something else' is.

1. To study about this situation, we first need to constrain the rigid body
• We have to constrain it in such a way that, it cannot have translational motion
2. The most effective way to achieve this, is to fix it along a straight line
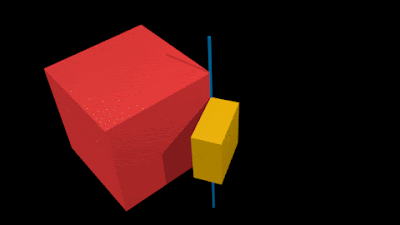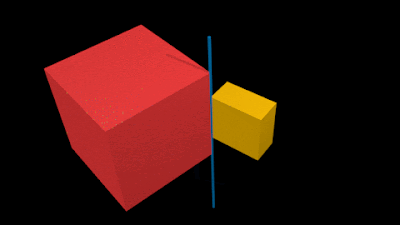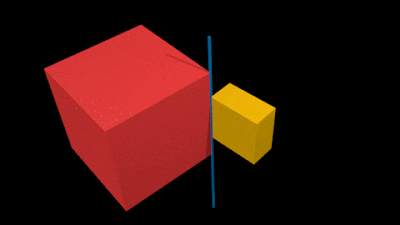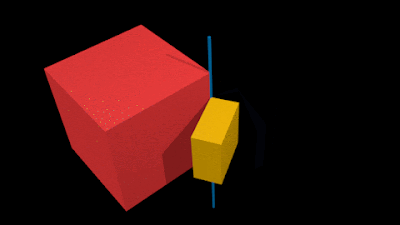
• The animation in fig.7.5 below shows an example:

Fig.7.5

• The small yellow rigid block is attached to the larger red rigid block
3. The attachment is along an edge. This edge is highlighted by a blue line
• This blue line is the 'straight line' along which the yellow block is fixed
• Because of this 'fixity', the yellow block cannot have translational motion
■ When a rigid body is fixed along a line, only one type of motion is possible for that body:
The rotational motion
(If in the above fig.7.5, the large red block was absent, the yellow block can complete a full 360^o rotation)
■ The line along which the rigid body is fixed is called it's axis of rotation
• Note that, the axis of rotation need not pass through the geometric center of the body 

---

In our day to day life, we come across many examples where rigid bodies rotate about an axis. let us see some of them:

Example 1: The ceiling fan
An animation of a 'rotating ceiling fan' is shown in fig.7.6 below

Fig.7.6

• The axis of rotation passes through the center of the ceiling fan. it is shown in fig.7.7 below:

Fig.7.7

• The axis is indicated by the blue straight line  
• The blue curved arrow indicates the direction of rotation
• The fan is fixed along the axis
■ If during rotation, the 'mechanism which fixes the axis' fails, the fan will move with both rotation and translation, causing serious accidents
• So we see that, fixity along the axis is important to ensure pure rotation 

Example 2: The potter's wheel
An animation of a rotating potter's wheel is shown in fig.7.8 below:

Fig.7.8

• The axis of rotation passes through the center of the wheel. It is shown in fig.7.9 below:

Fig.7.9

• The axis is indicated by the blue straight line  
• The curved arrow indicates the direction of rotation
■ If the 'mechanism which fixes the axis' fails, the wheel will move with both rotation and translation
• So we see that, fixity along the axis is important to ensure pure rotation 

Characteristics of rotational motion

1. The animation in fig.7.10 below, shows a rotating body

Fig.7.10

• The axis of rotation is shown in blue color
■ For convenience of mathematical calculations, we will consider this axis to be the 'z-axis' of the 'frame of reference'
    ♦ The x-axis is shown in red color
    ♦ The y-axis is shown in green color
2. We are inclined to think that: Every particle in the body will be in rotation
• But that is not entirely true. Let us see the reason:
• We will consider 3 particles inside the body
    ♦ They are indicated by small spheres
    ♦ The red, yellow and green spheres
3. If we trace the path of the red sphere, that path will be a circle
• It is the red circle that we see in the animation
• What is the radius of this circle?
• Obviously, radius = distance of the red sphere from the axis
• We will denote it as r_R
4. If we trace the path of the yellow sphere, it will be a circle
• It is the yellow circle that we see in the animation
• What is the radius of this circle?
• Obviously, radius = distance of the yellow sphere from the axis
• We will denote it as r_Y
5. If we try to trace the path of the green sphere, we will not succeed
• This is because there is no such path
• In other words, there is no green circle. That is., r_G = 0
• 'No path' means that, there is no movement. That is., the green sphere is stationary
■ Like the green sphere, all the particles which lie on the axis are stationary. This is the answer to the doubt mentioned in (2) above
6. So we have two circles: The red circle and the yellow circle
• We know that, any circle will be having it's own plane
• The plane in which the red circle lies, is shown in red color in fig.7.11(a) below

Fig.7.11

• The plane in which the yellow circle lies, is shown blue color in fig.b.
• The plane of the red circle is perpendicular to the axis of rotation
    ♦ This is indicated by the white set-square in fig.a
• The plane of the yellow circle is also perpendicular to the axis
    ♦ This is indicated by the white set-square in fig.b

---

Let us write a summary of the 'characteristics of rotational motion':

■ If a rigid body is in rotation about an axis, then:
• Every particle of the body, which lies on the axis will be stationary
• Each of the other particles will be rotating in it's own circular path
    ♦ The center of that circular path lies on the axis
    ♦ Radius of that circular path = Distance of the particle from the axis
• That circular path lies on a plane
    ♦ This plane is perpendicular to the axis

---

Also it is worth mentioning that, in the animation in fig.7.10 above, the red sphere moves with a greater speed than the yellow sphere
This is because, r_R > r_Y
We saw the detailed explanation in a previous section.

---

In the next section, we will see another type of rotational motion

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved

Chapter 7 - Systems of Particles And Rotational Motion

In the previous section, we completed a discussion on two-dimensional collision. In this chapter, we will see rotational motion.

• In the previous chapters, we analyzed many cases in which ‘objects’ are involved. Let us recall some examples that we have seen:
    ♦ An object acted upon by a net force moves from one position to another
    ♦ A projectile moving in a parabolic path is acted upon by various forces
    ♦ An object at a height possess potential energy
    ♦ An object moving with a certain velocity possess kinetic energy
    ♦ Collision between objects causes changes in their original velocities     
so on . . .
• In all those cases, we considered the objects to be point masses
    ♦ It is true that, we drew them not as points, but as squares, rectangles, spheres, cars, trucks, etc.,
    ♦ But we drew the vectors from their centers
    ♦ We assumed that, all the mass of an object is concentrated at the 'center point' 

---

■ ‘Point mass’ can be explained as follows:
• If an object is said to have a mass ‘m’ kg, all that mass is assumed to be concentrated at a point
• That point is a ‘point mass’  
• Even though it is a ‘point’, it's mass is not zero
• Considering objects to be point masses helps to simplify calculations

---

• So we can do calculations by two methods:
(i) Considering an object to be a point mass
(ii) Considering the actual distribution of mass in the object
• On many occasions, the results obtained by the two methods will not be appreciably different
■ If we consider the ‘actual distribution of mass’ in an object, then it is called an extended object
• While considering an extended object, it’s size becomes important
    ♦ It cannot be considered as a point
• So basically, an ‘extended object’ is a ‘system of particles’
• In some problems in physics, it is compulsory to consider objects as ‘extended objects’
• In fig.7.1(a) below, a cube is shown. 

Fig.7.1

• It is a uniform cube. That is., the mass is distributed uniformly through out the entire volume of the cube. 
• In such cases, we can consider the cube to be a point mass located at the 'geometric center' of the cube. 
• The geometric center of a cube is easy to locate. Recall that, in many diagrams that we saw in the previous chapters, we drew velocity vectors, force vectors etc., through the geometric center of the objects. 
• Now consider fig.b. Geometrically, it is a cube. But more mass is concentrated towards the left side.
• That is., the 'left side is heavier' and 'right side is lighter'. We cannot consider the mass to be concentrated at the geometric center. If we make such an assumption, the results will not be correct 
• In such cases, we need to define a new ‘point’
■ This point is called the ‘center of mass’
• So we have two points:
    ♦ A point which is the geometric center
    ♦ A point which is the center of mass
• Unlike the ‘geometric center’, the ‘center of mass’ is not easy to find
• However in later sections, we will see methods to find it for 'simple objects'

Significance of Rigid bodies

Following the above discussion, we encounter a new ‘situation’. It can be explained as follows:
Consider a scenario in steps:
1. We have to solve a problem involving an extended object
2. We start off by calculating the center of mass of that object
• An example is shown in fig.7.2(a) below:

Fig.7.2

• The center of mass is denoted by the red '❌' mark
3. But when a force act on the object, it gets deformed
• As a result, the center of mass shifts to a new position. This is shown in fig.7.2(b)
• We will have to recalculate the new position

---

Such a difficulty can be overcome by assuming the object to be ‘rigid’

■ A rigid body is a body with a perfectly definite and unchanging shape
• Consider any one 'pair of points' in that body
    ♦ The distance between the points in that pair, will not change

---

• However, no real body is truly rigid. Because, all of them deforms under the influence of forces
• But in many cases, those deformations are negligible
• We can confidently do problems by considering them to be rigid
• We will learn about advanced cases (where deformations also have to be considered) in higher classes

Motion of a rigid body

1. Consider a rigid block shown in fig.7.3(a) below:

Fig.7.3

• It moves with uniform velocity $\mathbf\small{\vec{v}}$ on a horizontal surface
2. Consider any two points P and Q in the body
We can write three detailed steps as follows:
(i) Let  $\mathbf\small{\vec{v}_P}$ be the velocity with which the point P moves
(ii) Let  $\mathbf\small{\vec{v}_Q}$ be the velocity with which the point Q moves
(iii) Then $\mathbf\small{\vec{v}_P=\vec{v}_Q=\vec{v}}$
• The result in (iii) is obvious. In fact we do not even need to write the three detailed steps. We know it is true
3. The same block is shown in fig.b
• But this time it moves with a non-uniform velocity
• For example, if it is moving with an acceleration 'a', we can say that, it is moving with a non-uniform velocity
• In such a situation, the velocity of the block will be different at different instances
4. A point 'A' is marked on the horizontal surface on which the block moves
• Let the velocity of the block at the instant when it just passes 'A' be $\mathbf\small{\vec{v}_{(A)}}$
• We can write three detailed steps as follows:
(i) Let $\mathbf\small{\vec{v}_{P(A)}}$ be the 'velocity with which the point P moves' at the instant when the block just passes 'A'
(ii) Let $\mathbf\small{\vec{v}_{Q(A)}}$ be the 'velocity with which the point Q moves' at the instant when the block just passes 'A'
(iii) Then $\mathbf\small{\vec{v}_{P(A)}=\vec{v}_{Q(A)}=\vec{v}_{(A)}}$
• The result in (iii) is obvious. In fact we do not even need to write the three detailed steps. We know it is true

---

If at any instant, all particles of a body have the same velocity, then that body is said to be in pure translational motion

---

Now we will see another type of motion:
1. Consider the side view of a cylinder in fig.7.4(a) below:

Fig.7.4

• It is rolling towards the right, on a horizontal surface. This 'rolling' is indicated by the white curved arrow

2. A point 'A' is marked on the horizontal surface on which the cylinder rolls
• Consider the instant at which the cylinder passes 'A' 
• A normal is drawn to the horizontal surface at A. It is shown in red color
• Also, this normal passes through the center O of the cylinder
3. Consider any two points P and Q on this normal
We can write three detailed steps as follows:
(i) Let $\mathbf\small{\vec{v}_{P(A)}}$ be the 'velocity with which the point P moves' at the instant when the cylinder just passes 'A'
(ii) Let $\mathbf\small{\vec{v}_{Q(A)}}$ be the 'velocity with which the point Q moves' at the instant when the cylinder just passes 'A'
(iii) Then $\mathbf\small{\vec{v}_{P(A)}\neq \vec{v}_{Q(A)}}$
4. In 3(iii), We have an inequality
• Unlike the previous cases that we saw about the block, this result is not so obvious. We need to give a bit of explanation
• The explanation can be written based on the second fig.b, as follows:
(i) In fig.b, a circle is drawn through P
• The center of this circle is 'O', which is the center of the cylinder
    ♦ $\mathbf\small{\vec{v}_{P(A)}}$ will be tangential to this circle
    ♦ $\mathbf\small{\vec{v}_{P(A)}}$ will be perpendicular to the red line
• Another circle is drawn through Q. The center of this circle also is 'O'
    ♦ $\mathbf\small{\vec{v}_{Q(A)}}$ will be tangential to this circle
    ♦ $\mathbf\small{\vec{v}_{Q(A)}}$ will be perpendicular to the red line
(ii) Since both the velocities are perpendicular to the red line, we can write:
• $\mathbf\small{\vec{v}_{P(A)}}$ and $\mathbf\small{\vec{v}_{Q(A)}}$ have the same direction
(iii) But their magnitudes will be different. Let us see the reason:
• Let $\mathbf\small{\omega_{(A)}}$ be the instantaneous angular velocity when the cylinder just passes 'A'
• This instantaneous angular velocity will be same for both P and Q
• It is the linear speeds $\mathbf\small{|\vec{v}_{P(A)}|}$ and $\mathbf\small{|\vec{v}_{Q(A)}|}$ which differ
• This difference is due to the 'greater radius' of the circle through P
• We saw a detailed explanation in a previous chapter
(v) For two vectors to be equal, both their magnitudes and directions should be equal
• In our present case, magnitudes are not equal
• This explains the result in 3(iii) that we saw above
5. Let us go back to fig.(a). Besides P and Q, one more point R is also marked
• It is on a violet line passing through O
6. In fig.c, a circle is drawn through R
• The center of this circle is O
• The instantaneous velocity $\mathbf\small{\vec{v}_{R(A)}}$ for R is tangential to this circle
• Also this $\mathbf\small{\vec{v}_{R(A)}}$ is perpendicular to the violet line
• Obviously, the direction of $\mathbf\small{\vec{v}_{R(A)}}$ is different from those of $\mathbf\small{\vec{v}_{P(A)}}$ and $\mathbf\small{\vec{v}_{Q(A)}}$
• Thus we can write: $\mathbf\small{\vec{v}_{P(A)}\neq \vec{v}_{Q(A)}\neq \vec{v}_{R(A)}}$
7. The rolling cylinder is at point 'A' that we marked on the horizontal surface
• If we mark another point 'B' to the right of 'A', after a short time, the cylinder will surely reach that 'B' 
• So we can say that the cylinder is in translational motion
• But all the particles in the cylinder are not moving with the same velocity
• So the cylinder is not in pure translational motion 
• It moves with: [Translation + ''something else']

---

In the next section, we will see what this 'something else' is.

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved

Chapter 6.25 - Two-Dimensional Collision - Examples

In the previous section, we discussed two-dimensional collision. We also saw a solved example. In this section, we will see a few more solved examples.

Solved example 6.40
Two objects 'A' and 'B' have masses 5 kg and 2.5 kg respectively. 'A' moves with a velocity of 4.5 ms^-1 towards 'B' which is initially at rest. After the collision, object 'A' moves in a direction which makes 30^o with it's original direction. Object 'B' moves in a direction which makes -30^o with the original direction of 'A'. Find the final velocities of 'A' and 'B'. Is the collision elastic or inelastic?
Solution:
1. Fig.6.80 below shows the collision:

Fig.6.80

2. The table is shown below:

• All the cells in columns 1 to 5 can be filled up (using the given data) except (A,3) and (B,3)
    ♦ (A,3) contains the unknown $\mathbf\small{|\vec{v_{Af}}|}$
    ♦ (B,3) contains the unknown $\mathbf\small{|\vec{v_{Bf}}|}$
• So there are two unknowns. We need to form two equations only
• Also note that, there are two 'question marks' in the fig.6.80 above
3. Considering momenta in the x-direction, we have:
• Sum in column 6 = Sum in column 8
$\mathbf\small{\Rightarrow [22.5+0]=[5|\vec{v_{Af(x)}}|+2.5|\vec{v_{Bf(x)}}|]}$
$\mathbf\small{\Rightarrow [22.5]=[5|\vec{v_{Af}}| \cos \theta_{Af}+2.5|\vec{v_{Bf}}| \cos \theta_{Bf}]}$
$\mathbf\small{\Rightarrow [22.5]=[5|\vec{v_{Af}}| \cos 30+|\vec{v_{Bf}}| \cos (-30)]}$
Dividing both sides by 2.5, we get:
$\mathbf\small{[9]=[2|\vec{v_{Af}}| \cos 30+|\vec{v_{Bf}}| \cos (-30)]}$
$\mathbf\small{\Rightarrow [9]=[1.732|\vec{v_{Af}}|+0.866|\vec{v_{Bf}}| ]}$
4. Considering momenta in the y-direction, we have:
• Sum in column 7 = Sum in column 9
$\mathbf\small{\Rightarrow [0]=[5|\vec{v_{Af(y)}}|+2.5|\vec{v_{Bf(y)}}|]}$
$\mathbf\small{\Rightarrow [0]=[5|\vec{v_{Af}}| \sin 30+|\vec{v_{Bf}}| \sin (-30)]}$
Deviding both sides by 2.5, we get:
$\mathbf\small{\Rightarrow [0]=[2|\vec{v_{Af}}| \sin 30+|\vec{v_{Bf}}| \sin (-30)]]}$
$\mathbf\small{\Rightarrow [0]=[2|\vec{v_{Af}}| 0.5+|\vec{v_{Bf}}| (-0.5)]}$
$\mathbf\small{\Rightarrow [0]=[|\vec{v_{Af}}|-.5|\vec{v_{Bf}}|]}$
5. So we have two equations:
(i) From (3) we have: $\mathbf\small{1.732|\vec{v_{Af}}|+0.866|\vec{v_{Bf}}|=9}$
(ii) From (4) we have: $\mathbf\small{|\vec{v_{Af}}|-0.5|\vec{v_{Bf}}|=0}$
• To solve the equations, the following steps can be used:
    ♦ Multiply (i) by '0.5'
    ♦ Multiply (ii) by 0.866
    ♦ Add the results 
• We get:
v_Af = 2.598 ms^-1
v_Bf = 5.196 ms^-1
6. Let us check whether it is an elastic collision or not:
• Applying law of conservation of kinetic energy, we have:
$\mathbf\small{\frac{1}{2}m_A|\vec{v}_{Ai}|^2+\frac{1}{2}m_B|\vec{v}_{Bi}|^2=\frac{1}{2}m_A|\vec{v}_{Af}|^2+\frac{1}{2}m_B|\vec{v}_{Bf}|^2}$
• Let us first calculate the LHS:
$\mathbf\small{\frac{1}{2}m_A|\vec{v}_{Ai}|^2+\frac{1}{2}m_B|\vec{v}_{Bi}|^2=\frac{1}{2}\times 5 \times 4.5^2+\frac{1}{2}\times 2.5 \times0^2=50.625\; \text{J}}$
• Next we calculate the RHS:
$\mathbf\small{\frac{1}{2}m_A|\vec{v}_{Af}|^2+\frac{1}{2}m_B|\vec{v}_{Bf}|^2=\frac{1}{2}\times 5 \times 2.598^2+\frac{1}{2}\times 2.5 \times 5.196^2=50.628\; \text{J}}$
■ We get: LHS = RHS
So kinetic energy is conserved and so it is an elastic collision

---

• We saw solved example 6.39 in the previous section
• We saw solved example 6.40 above in the present section
• Both of those examples involves only two unknowns
• Such problems can be easily solved using two equations that we obtain from the law of conservation of momentum
■ The calculations become even more easier if the two objects stick together after collision
• Let us see such a problem: 

Solved example 6.41
Car A has a mass of 1800 kg. It moves towards the North with a velocity of 15 ms^-1. Car B has a mass of 1500 kg. It moves in a South-East direction, making an angle of 30^o with the East-West direction. It has a velocity of 10 ms^-1. After collision, they stick together. Find the velocity (magnitude and direction) of the combined mass after the collision
Solution:
1. Fig.6.81 below shows the collision:

Fig.6.81

• East-West direction can be taken as the x-axis
2. The table is shown below:

• The first 5 columns can be filled up using the given data
• However, be careful while filling column 4
    ♦ Velocity of 'A' makes an angle of 90^o with the East-West direction (the x-axis)
    ♦ So we have '90' in the cell (A,4)
    ♦ Velocity of 'B' makes an angle of 30^o with the x-axis
    ♦ So we have '30' in the cell (B,4)
    ♦ sin 30 is not negative
    ♦ But we must put a negative value in the cell (B,7)
    ♦ This is because, that velocity is towards the negative side of the y-axis
• After collision, both cars move together. So they will be having the same velocity
    ♦ Thus we have: $\mathbf\small{|\vec{v}_{Af}|=|\vec{v}_{Bf}|}$
    ♦ We can put: $\mathbf\small{|\vec{v}_{Af}|=|\vec{v}_{Bf}|=|\vec{v}_{f}|}$ 
    ♦ We see this in the cells (A,3) and (B,3)
• After collision, since they move together with the same velocity, they will be making the same angle with the x axis
    ♦ Thus we have: $\mathbf\small{\theta_{Af}=\theta_{Bf}}$
    ♦ We can put: $\mathbf\small{\theta_{Af}=\theta_{Bf}=\theta_{f}}$ 
    ♦ We see this in the cells (A,5) and (B,5)
• After filling the first five columns, we see that there are two unknowns. So we need to form two equations only
• Also note that, there are two 'question marks' in the fig.6.81 above
3. Considering momenta in the x-direction, we have:
• Sum in column 6 = Sum in column 8
$\mathbf\small{\Rightarrow [0+12990]=[1800|\vec{v_{f(x)}}|+1500|\vec{v_{f(x)}}|]}$
$\mathbf\small{\Rightarrow [12990]=[(1800+1500)|\vec{v_{f(x)}}|]}$
$\mathbf\small{\Rightarrow [12990]=[3300|\vec{v_{f(x)}}|]}$
$\mathbf\small{\Rightarrow |\vec{v}_{f(x)}|=\frac{12990}{3300}=3.936\;\text{ms}^{-1}}$
4. Considering momenta in the y-direction, we have:
• Sum in column 7 = Sum in column 9
$\mathbf\small{\Rightarrow [27000-7500]=[1800|\vec{v_{f(y)}}|+1500|\vec{v_{f(y)}}|]}$
$\mathbf\small{\Rightarrow [19500]=[(1800+1500)|\vec{v_{f(y)}}|]}$
$\mathbf\small{\Rightarrow [19500]=[3300|\vec{v_{f(y)}}|]}$
$\mathbf\small{\Rightarrow |\vec{v}_{f(y)}|=\frac{19500}{3300}=5.91\;\text{ms}^{-1}}$
5. Now we can find the magnitude of the resultant
$\mathbf\small{|\vec{v}_{f}|=\sqrt{|\vec{v}_{fx}|^2+|\vec{v}_{fy}|^2}=\sqrt{3.936^2+5.91^2}=7.1\;\text{ms}^{-1}}$
6. Direction of this resultant is given by: $\mathbf\small{\tan \theta_f=\frac{|\vec{v}_{fy}|}{|\vec{v}_{fx}|}=\frac{5.91}{3.936}=1.501}$
$\mathbf\small{\Rightarrow \theta_f=\tan^{-1}1.501=56.33^\text{o}}$
7. Thus we can write:
■ The final velocity shown in fig.6.81 has a magnitude of 7.1 ms^-1 and a direction which makes 56.33^o with the x-axis

---

• Next we will see problems with 3 unknowns.  Such problems involve somewhat lengthy calculations
■ But those calculations will be greatly simplified if the two colliding objects have the same mass
• The Solved examples 6.42 and 6.43 given below will demonstrate this idea

Solved example 6.42
Prove that an elastic collision between equal masses in 2 dimensions always results in the objects bouncing off each other at a 90^o degrees angle (assume one of the objects to be initially stationary). 
Solution:
1. Fig.6.82 below shows a 2-dimensional collision between two spheres 'A' and 'B'

Fig.6.82

• Both the spheres have the same mass. So we can write: m_A = m_B = m
• We have to prove that $\mathbf\small{(\theta_{Af}+\theta_{Bf})=90^\text{o}}$
2. The table is shown below:

3. Considering momenta in the x-direction, we have:
• Sum in column 6 = Sum in column 8
$\mathbf\small{\Rightarrow \sum |\vec{p}_{i(x)}|=\sum |\vec{p}_{f(x)}|}$
$\mathbf\small{\Rightarrow [m|\vec{v}_{Ai(x)}|+0]=[m|\vec{v}_{Af(x)}|+m|\vec{v}_{Bf(x)}|]}$
$\mathbf\small{\Rightarrow [|\vec{v}_{Ai(x)}|]=[|\vec{v}_{Af(x)}|+|\vec{v}_{Bf(x)}|]}$
$\mathbf\small{\Rightarrow [|\vec{v}_{Ai}|\cos \theta_{Ai}]=[|\vec{v}_{Af}|\cos \theta_{Af}+|\vec{v}_{Bf}|\cos \theta_{Bf}]}$
4. Considering momenta in the y-direction, we have:
• Sum in column 7 = Sum in column 9
$\mathbf\small{\Rightarrow \sum |\vec{p}_{i(y)}|=\sum |\vec{p}_{f(y)}|}$
$\mathbf\small{\Rightarrow [0+0]=[m|\vec{v}_{Af(y)}|+m|\vec{v}_{Bf(y)}|]}$
$\mathbf\small{\Rightarrow [0]=[|\vec{v}_{Af(y)}|+|\vec{v}_{Bf(y)}|]}$
$\mathbf\small{\Rightarrow [0]=[|\vec{v}_{Af}|\sin \theta_{Af}+|\vec{v}_{Bf}|\sin \theta_{Bf}]}$
5. So we have two equations:
(i) From (3) we have: $\mathbf\small{|\vec{v}_{Af}|\cos \theta_{Af}+|\vec{v}_{Bf}|\cos \theta_{Bf}=|\vec{v}_{Ai}|\cos \theta_{Ai}}$
(ii) From (4) we have: $\mathbf\small{|\vec{v}_{Af}|\sin \theta_{Af}+|\vec{v}_{Bf}|\sin \theta_{Bf}=0}$
6. But we have three unknowns. So we must have three equations
• For the third equation, we apply conservation of kinetic energy
• Total initial kinetic energy = Total final kinetic energy
• Since the masses are equal, we have: $\mathbf\small{|\vec{v_{Ai}}|^2+|\vec{v_{Bi}}|^2=|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2}$
$\mathbf\small{\Rightarrow |\vec{v_{Ai}}|^2=|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2}$
[∵ v_Bi = 0]
7. Let us write the three equations together:
(i) From (3) we have: $\mathbf\small{|\vec{v}_{Af}|\cos \theta_{Af}+|\vec{v}_{Bf}|\cos \theta_{Bf}=|\vec{v}_{Ai}|\cos \theta_{Ai}}$
(ii) From (4) we have: $\mathbf\small{|\vec{v}_{Af}|\sin \theta_{Af}+|\vec{v}_{Bf}|\sin \theta_{Bf}=0}$

(iii) From (6) we have: $\mathbf\small{|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2=|\vec{v_{Ai}}|^2}$

8. Let us write them in a 'easy to manipulate' form:
(i) $\mathbf\small{A\;\cos \theta_{A}+B\cos \theta_{B}=k_1}$
(ii) $\mathbf\small{A\;\sin \theta_{A}+B\sin \theta_{B}=0}$
(iii) $\mathbf\small{A^2+B^2=(k_1)^2}$ 
Where:
• $\mathbf\small{A=|\vec{v_{Af}}|}$. A quantity that we have to find
• $\mathbf\small{B=|\vec{v_{Bf}}|}$. A quantity that we have to find
• $\mathbf\small{\theta_{B}=\theta_{B_f}}$. A quantity that we have to find
• $\mathbf\small{\theta_{A}=\theta_{Af}}$. A constant, which can be calculated from the given data

• $\mathbf\small{k_1=|\vec{v}_{Ai}|\cos \theta_{Ai}}$ 
    ♦ But $\mathbf\small{\theta_{Ai}=0}$. So $\mathbf\small{\cos \theta_{Ai}}$ =1
    ♦ Thus we get: $\mathbf\small{k_1=|\vec{v}_{Ai}|\cos \theta_{Ai}=|\vec{v}_{Ai}|}$ 
    ♦ So k₁ is a constant, which can be calculated from the given data

■ Now we can write the steps for obtaining the 3 unknowns:
(iv) Squaring (i), we get:
$\mathbf\small{A^2\,\cos^2\theta_A+B^2\,\cos^2\theta_B+2AB\,\cos\theta_A\,\cos\theta_B=(k_1)^2}$
(v) Squaring (ii), we get:
$\mathbf\small{A^2\,\sin^2\theta_A+B^2\,\sin^2\theta_B+2AB\,\sin\theta_A\,\sin\theta_B=0}$
(vi) Adding (iv) and (v), we get:
$\mathbf\small{(A^2\,\cos^2\theta_A+A^2\,\sin^2\theta_A)+(A^2\,\sin^2\theta_B+B^2\,\sin^2\theta_B)+(2AB\,\cos\theta_A\,\cos\theta_B+2AB\,\sin\theta_A\,\sin\theta_B)=(k_1)^2+0}$
$\mathbf\small{\Rightarrow A^2(\cos^2\theta_A+\sin^2\theta_A)+B^2(\sin^2\theta_B+\sin^2\theta_B)+(2AB\,\cos\theta_A\,\cos\theta_B+2AB\,\sin\theta_A\,\sin\theta_B)=(k_1)^2+0}$
$\mathbf\small{\Rightarrow A^2+B^2+(2AB\,\cos\theta_A\,\cos\theta_B+2AB\,\sin\theta_A\,\sin\theta_B)=(k_1)^2}$
(vii) But from (iii), we have: $\mathbf\small{A^2+B^2=(k_1)^2}$
• Substituting this in (v), we get:
$\mathbf\small{(k_1)^2+(2AB\,\cos\theta_A\,\cos\theta_B+2AB\,\sin\theta_A\,\sin\theta_B)=(k_1)^2}$
$\mathbf\small{\Rightarrow 2AB\,\cos\theta_A\,\cos\theta_B+2AB\,\sin\theta_A\,\sin\theta_B=0}$
$\mathbf\small{\Rightarrow 2AB(\cos\theta_A\,\cos\theta_B+\,\sin\theta_A\,\sin\theta_B)=0}$
(viii) Using the identity $\mathbf\small{\cos(\theta_1-\theta_2)=\cos\theta_1\,\cos\theta_2+\sin\theta_1\,\sin\theta_2}$, we get:
$\mathbf\small{2AB\,\cos(\theta_A-\theta_B)=0}$
(ix) Putting back the values, we get:
• $\mathbf\small{2|\vec{v}_{Af}|\,|\vec{v}_{Bf}|\,\cos(\theta_{Af}-\theta_{Bf})=0}$
• $\mathbf\small{|\vec{v}_{Af}|}$ can be zero only if all the three conditions given below are satisfied:
    ♦ It is a one-dimensional collision (Details here)
    ♦ The two masses are equal
    ♦ Object B is stationary before collision
• In our present case, the second and third conditions are satisfied
• But it is not a one-dimensional collision. What we have is a two-dimensional collision
• So $\mathbf\small{|\vec{v}_{Af}|}$ cannot be zero  
• $\mathbf\small{|\vec{v}_{Bf}|}$ can be zero only if the mass of B is very large compared to mass of A. But in our present case, both masses are equal
• So $\mathbf\small{|\vec{v}_{Bf}|}$ cannot be zero
• Thus the only option is: $\mathbf\small{\cos(\theta_{Af}-\theta_{Bf})=0}$
• If $\mathbf\small{\cos(\theta_{Af}-\theta_{Bf})=0}$, then $\mathbf\small{(\theta_{Af}-\theta_{Bf})=90^\text{o}}$  
■ This relation $\mathbf\small{(\theta_{Af}-\theta_{Bf})=90^\text{o}}$ is our key
9. In fig.6.83(a) below, we see that, $\mathbf\small{(\theta_{Af}-\theta_{Bf})}$ is the 'angle between the two final vectors'

Fig.6.83

• If $\mathbf\small{(\theta_{Af}-\theta_{Bf})}$ is to be 90, the 'after collision' fig. will be as in (b)
• Here also, $\mathbf\small{(\theta_{Af}-\theta_{Bf})}$ is the 'angle between the two final vectors'

10. Another possibility is shown in fig.c

• After collision, the object 'B' is below the x-axis. It's final velocity vector makes an angle of $\mathbf\small{-\theta_{Bf}}$ with the x-axis  
• So $\mathbf\small{(\theta_{Af}-\theta_{Bf})}$ becomes: $\mathbf\small{[\theta_{Af}-(-\theta_{Bf})]=[theta_{Af}+\theta_{Bf}]}$ 
• Here also, $\mathbf\small{(\theta_{Af}-\theta_{Bf})}$ is the 'angle between the two final vectors'
■ Thus we can write: After a 2-dimensional collision, the two objects will scatter at 90^o to each other when the following two conditions are satisfied:
    ♦ The two objects have the same mass
    ♦ One of the objects is stationary before collision

Solved example 6.43
Two identical objects A and B collide on a smooth horizontal surface. B was originally at rest. A has an initial velocity of 6 ms^-1. After collision it scatters at an angle of 30^o to the original direction.
(a) What is the magnitude of the velocity of 'A' after the collision ?
(b) What is the magnitude and direction of the velocity of 'B' after the collision ?
Solution:
1. Fig.6.84 below shows the collision:

Fig.6.84

• In the fig.6.84, θ_Bf is shown below the initial direction. But the initial direction is considered as the x-axis
• So θ_Bf is below the x-axis. That means, θ_Bf is negative
• But we need not write '(-θ_Bf)' and do the calculations. We can do the calculations using '(+θ_Bf)'
• If in the final results, we get a negative value for 'θ_Bf', the positions in fig.6.83 will be justified
2. The table is shown below:

• All the cells in columns 1 to 5 can be filled up (using the given data) except (A,3), (B,3) and (B,5)
    ♦ (A,3) contains the unknown $\mathbf\small{|\vec{v_{Af}}|}$
    ♦ (B,3) contains the unknown $\mathbf\small{|\vec{v_{Bf}}|}$
    ♦ (B,5) contains the unknown $\mathbf\small{\theta_{Bf}}$
• So there are three unknowns. We need to form three equations
• Also note that, there are 3 'question marks' in the fig.6.84 above
• Most of the cells in columns 6 to 9 need to be calculated except (B,6), (A,7) and (B,7)
• Those 3 cells have zero values because:
    ♦ B has zero initial x-velocity
    ♦ A has zero initial y-velocity
    ♦ B has zero initial y-velocity
3. Considering momenta in the x-direction, we have:
• Sum in column 6 = Sum in column 8
$\mathbf\small{\Rightarrow [6m+0]=[m|\vec{v_{Af(x)}}|+m|\vec{v_{Bf(x)}}|]}$
$\mathbf\small{\Rightarrow [6]=[|\vec{v_{Af}}| \cos \theta_{Af}+|\vec{v_{Bf}}| \cos \theta_{Bf}]}$
$\mathbf\small{\Rightarrow [6]=[|\vec{v_{Af}}| \cos 30+|\vec{v_{Bf}}| \cos \theta_{Bf}]}$
$\mathbf\small{\Rightarrow [6]=[0.866|\vec{v_{Af}}|+|\vec{v_{Bf}}| \cos \theta_{Bf}]}$
4. Considering momenta in the y-direction, we have:
• Sum in column 7 = Sum in column 9
$\mathbf\small{\Rightarrow [0]=[m|\vec{v_{Af(y)}}|+m|\vec{v_{Bf(y)}}|]}$
$\mathbf\small{\Rightarrow [0]=[|\vec{v_{Af}}| \sin \theta_{Af}+|\vec{v_{Bf}}| \sin \theta_{Bf}]}$
$\mathbf\small{\Rightarrow [0]=[|\vec{v_{Af}}| \sin 30+|\vec{v_{Bf}}| \sin \theta_{Bf}]}$
$\mathbf\small{\Rightarrow [0]=[0.5|\vec{v_{Af}}|+|\vec{v_{Bf}}| \sin \theta_{Bf}]}$
5. So we have two equations:
(i) From (3) we have: $\mathbf\small{0.866|\vec{v_{Af}}|+|\vec{v_{Bf}}| \cos \theta_{Bf}=6}$
(ii) From (4) we have: $\mathbf\small{0.5|\vec{v_{Af}}|+|\vec{v_{Bf}}| \sin \theta_{Bf}=0}$
6. But we have three unknowns. So we must have three equations
• For the third equation, we apply conservation of kinetic energy
Total initial kinetic energy = Total final kinetic energy
• Since the masses are equal, we have: $\mathbf\small{|\vec{v_{Ai}}|^2+|\vec{v_{Bi}}|^2=|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2}$
$\mathbf\small{\Rightarrow |\vec{v_{Ai}}|^2+0=|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2}$
$\mathbf\small{\Rightarrow 6^2=|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2}$
$\mathbf\small{\Rightarrow |\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2=36}$
7. Let us write the three equations together:
(i) From (3) we have: $\mathbf\small{0.866|\vec{v_{Af}}|+|\vec{v_{Bf}}| \cos \theta_{Bf}=6}$
(ii) From (4) we have: $\mathbf\small{0.5|\vec{v_{Af}}|+|\vec{v_{Bf}}| \sin \theta_{Bf}=0}$
(iii) From (6) we have: $\mathbf\small{|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2=36}$

8. Now we apply the relation $\mathbf\small{\theta_{Af}-\theta_{Bf}=90^\text{o}}$
We get: $\mathbf\small{30-\theta_{Bf}=90}$
$\mathbf\small{\Rightarrow \theta_{Bf}=30-90=-60^\text{o}}$ 
• Note: We can apply this relation because, the following two conditions are satisfied:
    ♦ The two objects have the same mass
    ♦ One of the objects is stationary before collision
9. Substituting this value of $\mathbf\small{\theta_{Bf}}$ in (i), we get:
$\mathbf\small{0.866|\vec{v_{Af}}|+|\vec{v_{Bf}}| \cos (-60)=6}$
$\mathbf\small{\Rightarrow 0.866|\vec{v_{Af}}|+0.5|\vec{v_{Bf}}|=6}$
10. Substituting this value of $\mathbf\small{\theta_{Bf}}$ in (ii), we get:
$\mathbf\small{0.5|\vec{v_{Af}}|+|\vec{v_{Bf}}| \sin (-60)=0}$
$\mathbf\small{\Rightarrow 0.5|\vec{v_{Af}}|-0.866|\vec{v_{Bf}}|=0}$
11. Solving (9) and (10), we get:
$\mathbf\small{|\vec{v_{Af}}|}$ = 5.196 ms^-1
$\mathbf\small{|\vec{v_{Bf}}|}$ = 3
• Note: For solving, the following steps can be used:
    ♦ Multiply (9) by 0.866
    ♦ Multiply (10) by 0.5
    ♦ Add the results
12. Check:
• Let us substitute the velocities in (iii). We have:
$\mathbf\small{|\vec{v_{Af}}|^2+|\vec{v_{Bf}}|^2=36}$
• The LHS will be: $\mathbf\small{5.196^2+3^2=(27+9)=36}$
• RHS = 36
• So the results obtained in (11) are correct

---

We have completed this discussion on work, energy and power. In the next chapter, we will discuss about rotational motion

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved

Chapter 6.24 - Two-dimensional Collision

In the previous section, we completed a discussion on one-dimensional collision. In this section, we will see two-dimensional collision.

1. In the fig.6.75 below, four spheres A, B, P and Q rest on a smooth horizontal surface
    ♦ All the four spheres have the same mass
    ♦ All the four spheres have the same diameter 
• The horizontal surface is shown in green color
2. Sphere P moves towards sphere Q with a velocity of v_Pi
• v_Pi is indicated by the cyan arrow

Fig.6.75

3. Sphere Q is initially at rest 
• That is., v_Qi = 0
4. A white dashed line is drawn in alignment with v_Pi
• We see that, the white dashed line passes through the center of sphere Q
■ So we can say that, the collision between P and Q will be a one-dimensional collision
5. Now consider the sphere A
• It moves towards sphere B with a velocity of v_Ai
• v_Ai is indicated by the cyan arrow
6. Sphere B is initially at rest 
• That is., v_Bi = 0
7. A white dashed line is drawn in alignment with v_Ai
• We see that, the white dashed line does not pass through the center of sphere B
■ So we can say that, the collision between A and B will not be a one-dimensional collision

---

8. The fig.6.75 that we saw above is a 3D view
• It is not convenient to draw 3D views every time
• So we usually draw 2D views. 
9. 2D views are familiar to us. The spheres P and Q can be shown in 2D as in fig.6.76(a) below:

Fig.6.76

• This is the view that we will see when we look at the spheres from the side
• The green surface will appear as a thick green line
• The spheres will appear as circles 
• The area of the green surface will not be visible when we look from the side
• For the one-dimensional collision between P and Q, this 2D view is sufficient 
10. Next we look at the spheres A and B from the side. The 2D view will be as shown in fig.6.76(b)
■ Unfortunately, fig.6.76(b) does not convey the information that: 'Collision between A and B is not one-dimensional'. It looks as if, v_Ai passes through the center of sphere B
• So, if the collision is not one-dimensional, 'looking from the side' will not help
• We have to change our 'view point'
11. We have to look from 'above'
• The 2D view when looked from 'above' is shown in fig.6.77:

Fig.6.77

• Note that:
    ♦ In fig.6.76, where view is from 'side', the green surface appears as a 'thick green line'
    ♦ In fig.6.77, where view is from 'above', the green surface appears as a 'green rectangle'
• So in this type of 2D view, we can clearly see that the collision between A and B will not be one-dimensional
12. Now we can start the analysis of the collision
• In the fig.6.78 below, the conditions before and after collisions are shown separately

Fig.6.78

• The point of collision between the two spheres is shown by a red '❌' mark
13. After the collision, sphere A moves with a velocity of v_Af
• This v_Af makes a particular angle with the initial direction of A
• We will denote this angle as θ_Af
14. After the collision, sphere B moves with a velocity of v_Bf
• This v_Bf makes a particular angle with the initial direction of A
• We will denote this angle as θ_Bf
15. The movements after the collision are in different directions
• So it is no longer a one-dimensional problem. We cannot describe the motions using the 'x-axis' alone
• We will need both x and y axes
■ The collision in fig.6.78 is a two-dimensional collision.
• So from now on, we will use vector notations for the analysis
16. In these types of problems, it is always convenient to consider the x-axis to lie along the 'initial direction'
• In the fig.6.78, the white dashed line indicates the 'initial direction'
• So we can write:
    ♦ $\mathbf\small{\vec{v_{Af}}}$ makes an angle of θ_Af with the x axis
    ♦ $\mathbf\small{\vec{v_{Bf}}}$ makes an angle of θ_Bf with the x axis 
17. The information obtained so far can be written in a tabular form as shown below:

The above table has only 5 columns. We will add additional columns as and when more information become available
18. So let us continue:
• We will apply the law of conservation of momentum
• But momentum is a vector quantity. So we will consider the x and y directions separately
• First we consider the x direction:
(i) Initial momentum of A in the x direction
$\mathbf\small{\vec{p_{Ai(x)}}=m_A \times \text{initial velocity of A in the x-direction}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times \cos (\theta_{Ai})]\hat{i}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times \cos (0)]\hat{i}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times 1]\hat{i}}$
$\mathbf\small{=[m_A \times|\vec{v_{Ai}}|]\hat{i}}$
(ii) Initial momentum of B in the x direction
$\mathbf\small{\vec{p_{Bi(x)}}=m_B \times \text{initial velocity of B in the x-direction}}$
$\mathbf\small{=m_B \times [|\vec{v_{Bi}}|\times \cos (\theta_{Bi})]\hat{i}}$
$\mathbf\small{=m_B \times [0\times \cos (\theta_{Bi})]\hat{i}}$
= 0
• The above information about 'initial momentum in x direction' is entered as the sixth column as shown below:

• Note that, the 6th column can be filled up by using information from columns 1, 2 and 4
(cosine of the angle in column 4)
• So writing in the tabular form is indeed advantageous
19. Now we consider the y direction:
(i) Initial momentum of A in the y direction
$\mathbf\small{\vec{p_{Ai(y)}}=m_A \times \text{initial velocity of A in the y-direction}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times \sin (\theta_{Ai})]\hat{j}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times \sin (0)]\hat{j}}$
$\mathbf\small{=m_A \times [|\vec{v_{Ai}}|\times 0]\hat{j}}$
= 0
(ii) Initial momentum of B in the y direction
$\mathbf\small{\vec{p_{Bi(y)}}=m_B \times \text{initial velocity of B in the y-direction}}$
$\mathbf\small{=m_B \times [|\vec{v_{Bi}}|\times \sin (\theta_{Bi})]\hat{j}}$
$\mathbf\small{=m_B \times [0 \times \sin (\theta_{Bi})]\hat{j}}$
= 0
• The above information about 'initial momentum in y direction' is entered as the seventh column as shown below:

• Note that, the 7th column can be filled up by using information from columns 1, 2 and 4
(sine of the angle in column 4)
• So writing in the tabular form is indeed advantageous
20. Next we consider the final momentum:
• First we consider the x direction:
(i) Final momentum of A in the x direction
$\mathbf\small{\vec{p_{Af(x)}}=m_A \times \text{final velocity of A in the x-direction}}$
$\mathbf\small{=m_A \times [|\vec{v_{Af}}|\times \cos (\theta_{Af})]\hat{i}}$
$\mathbf\small{=[m_A \times|\vec{v_{Af}}|\times \cos (\theta_{Af})]\hat{i}}$
(ii) Final momentum of B in the x direction
$\mathbf\small{\vec{p_{Bf(x)}}=m_B \times \text{final velocity of B in the x-direction}}$
$\mathbf\small{=m_B \times [|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]\hat{i}}$
$\mathbf\small{=[m_B \times|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]\hat{i}}$
• The above information about 'final momentum in x direction' is entered as the 8th column as shown below:

• Note that, the 8th column can be filled up by using information from columns 1, 3 and 5
(cosine of the angle in column 5)
21. Next we consider the y direction:
(i) Final momentum of A in the y direction
$\mathbf\small{\vec{p_{Af(y)}}=m_A \times \text{final velocity of A in the y-direction}}$
$\mathbf\small{=m_A \times [|\vec{v_{Af}}|\times \cos (\theta_{Af})]\hat{i}}$
$\mathbf\small{=[m_A \times|\vec{v_{Af}}|\times \cos (\theta_{Af})]\hat{i}}$
(ii) Final momentum of B in the y direction
$\mathbf\small{\vec{p_{Bf(y)}}=m_B \times \text{final velocity of B in the y-direction}}$
$\mathbf\small{=m_B \times [|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]\hat{i}}$
$\mathbf\small{=[m_B \times|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]\hat{i}}$
• The above information about 'final momentum in x direction' is entered as the 9th column as shown below:

• Note that, the 9th column can be filled up by using information from columns 1, 3 and 5
(sine of the angle in column 5)
22. In our present case, this y component is negative because, it is directed towards the negative side of the x axis
• We will directly get this negative direction if we put 'negative value' for θ_Bf 
• For example, sin(-30) = -sin30 = -0.5
23. Now we apply the conservation of momentum in the x-direction. We have:
• Total initial momentum in the x-direction = Total final momentum in the x direction
That is., $\mathbf\small{\sum{|\vec{p_{i(x)}}|}=\sum{|\vec{p_{f(x)}}|}}$
$\mathbf\small{\Rightarrow|\vec{p_{iA(x)}}|+0=|\vec{p_{fA(x)}}|+|\vec{p_{fB(x)}}|}$
$\mathbf\small{\Rightarrow [m_A \times|\vec{v_{Ai}}|]=[m_A \times|\vec{v_{Af}}|\times \cos (\theta_{Af})]+[m_B \times|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]}$
• This equation can be easily formed from the table as follows:
Total from column 6 = Total from column 8
24. Next we apply the conservation of momentum in the y-direction. We have:
• Total initial momentum in the y-direction = Total final momentum in the y direction
That is., $\mathbf\small{\sum{|\vec{p_{i(y)}}|}=\sum{|\vec{p_{f(y)}}|}}$
$\mathbf\small{\Rightarrow0+0=|\vec{p_{fA(y)}}|+|\vec{p_{fB(y)}}|}$
$\mathbf\small{\Rightarrow 0=[m_A \times|\vec{v_{Af}}|\times \sin (\theta_{Af})]+[m_B \times|\vec{v_{Bf}}|\times \sin (\theta_{Bf})]}$
• This equation can be easily formed from the table as follows:
Total from column 7 = Total from column 9
25. With that, we complete our calculations related to momentum. Next we consider energy
• Assuming an elastic collision, we can say: 'kinetic energy will be conserved'
• Energy is a scalar quantity. There is no need to consider x and y components
• So we can write:
$\mathbf\small{\frac{1}{2}m_A\;|\vec{v_{Ai}}|^2+\frac{1}{2}m_B\;|\vec{v_{Bi}}|^2=\frac{1}{2}m_A\;|\vec{v_{Af}}|^2+\frac{1}{2}m_BA\;|\vec{v_{Bf}}|^2}$
$\mathbf\small{\Rightarrow m_A\;|\vec{v_{Ai}}|^2+m_B\;|\vec{v_{Bi}}|^2=m_A\;|\vec{v_{Af}}|^2+m_BA\;|\vec{v_{Bf}}|^2}$
26. So we have three equations:
(i) From (23), we have: $\mathbf\small{[m_A \times|\vec{v_{Ai}}|]=[m_A \times|\vec{v_{Af}}|\times \cos (\theta_{Af})]+[m_B \times|\vec{v_{Bf}}|\times \cos (\theta_{Bf})]}$

(ii) From (24), we have: $\mathbf\small{0=[m_A \times|\vec{v_{Af}}|\times \sin (\theta_{Af})]+[m_B \times|\vec{v_{Bf}}|\times \sin (\theta_{Bf})]}$

(iii) From (25), we have: $\mathbf\small{m_A\;|\vec{v_{Ai}}|^2+m_B\;|\vec{v_{Bi}}|^2=m_A\;|\vec{v_{Af}}|^2+m_BA\;|\vec{v_{Bf}}|^2}$
26. In the above 3 equations.
• Which are the 'known quantities' ? 
• Which are the 'unknown quantities' ? 
Let us analyse:
m_A - Known quantity. Will be given in the question
m_B - Known quantity. Will be given in the question
v_Ai - Known quantity. Will be given in the question
v_Bi - Known quantity. Will be given in the question
v_Af - Unknown quantity. A final quantity which we have to determine
v_Bf - Unknown quantity. A final quantity which we have to determine
θ_Af - Unknown quantity. A final quantity which we have to determine
θ_Bf - Unknown quantity. A final quantity which we have to determine
27. There are 4 unknowns. We have only 3 equations.
• So we use special 'angle measuring devices' to find one of the final angles θ_Af or θ_Bf
• Then the 'number of unknowns' will become 3.
• We can easily find the other unknowns
28. Further, if both the final angles are known, the 'number of unknowns' will reduce to 2
• In such cases we need to form the first two equations only

---

Let us see some solved examples:
Solved example 6.39
Two objects A and B have the same mass of 0.1 kg. Object A has an initial speed of 5 ms^-1. Object B is initially at rest. A collides with B and moves off with a speed of 2 ms^-1 at an angle of 30^o with the initial direction. What is the speed and direction of B?
Solution:
1. Fig.6.79 below shows the possible collision:

Fig.6.79

• In the above fig.6.79, θ_Bf is shown below the initial direction. But the initial direction is considered as the x-axis
• So θ_Bf is below the x-axis. That means, θ_Bf is negative
• But we need not write '(-θ_Bf)' and do the calculations. We can do the calculations using '(+θ_Bf)'
• If in the final results, we get a negative value for 'θ_Bf', the positions in fig.6.79 will be justified
2. The table is shown below:

• All the cells in columns 1 to 5 can be filled up (using the given data) except (B,3) and (B,5)
    ♦ (B,3) contains the unknown $\mathbf\small{|\vec{v_{Bf}}|}$
    ♦ (B,5) contains the unknown $\mathbf\small{\theta_{Bf}}$
• So there are only two unknowns. We need to form two equations only
• All the cells in columns 6 to 9 can be calculated except (B,8) and (B,9)  
3. Considering momenta in the x-direction, we have:
• Sum in column 6 = Sum in column 8
$\mathbf\small{\Rightarrow 0.5=0.173+|\vec{P_{Bf(x)}}|}$
$\mathbf\small{\Rightarrow 0.5=0.173+m_B\times|\vec{v_{Bf(x)}}|}$
$\mathbf\small{\Rightarrow 0.5=0.173+0.1\times|\vec{v_{Bf(x)}}|}$
$\mathbf\small{\Rightarrow |\vec{v_{Bf(x)}}|=3.27}$
$\mathbf\small{\Rightarrow |\vec{v_{Bf}}|\times \cos \theta_{Bf}=3.27}$
4. Considering the momenta in the y-direction, we have:
• Sum in column 7 = Sum in column 9
$\mathbf\small{\Rightarrow 0=0.1+|\vec{P_{Bf(y)}}|}$
$\mathbf\small{\Rightarrow 0=0.1+m_B\times|\vec{v_{Bf(y)}}|}$
$\mathbf\small{\Rightarrow 0=0.1+0.1\times|\vec{v_{Bf(y)}}|}$
$\mathbf\small{\Rightarrow |\vec{v_{Bf(y)}}|=-1}$
$\mathbf\small{\Rightarrow |\vec{v_{Bf}}|\times \sin \theta_{Bf}=-1}$
5. So we have two equations:
(i) From (3) we have: $\mathbf\small{|\vec{v_{Bf}}|\times \cos \theta_{Bf}=3.27}$ 
(ii) From (4) we have: $\mathbf\small{|\vec{v_{Bf}}|\times \sin \theta_{Bf}=-1}$ 
• Dividing 5(ii) by 5(i), we get:
$\mathbf\small{\frac{|\vec{v_{Bf}}|\times \sin \theta_{Bf}}{|\vec{v_{Bf}}|\times \cos \theta_{Bf}}=\frac{-1}{3.27}}$
$\mathbf\small{\Rightarrow \tan \theta_{Bf}=-\frac{1}{3.27}}$
$\mathbf\small{\Rightarrow \theta_{Bf}=-17^o}$
• θ_Bf is negative. So the positions in fig.6.79 are justified
6. Substituting this value of θ_Bf in 5(i), we get:
$\mathbf\small{|\vec{v_{Bf}}|\times \cos (-17)=3.27}$
$\mathbf\small{\Rightarrow |\vec{v_{Bf}}|=\frac{3.27}{\cos (-17)}=\frac{3.27}{0.9563}=3.42\,\,\text{ms}^{-1}}$

---

We have completed this discussion on work, energy and power. In the next chapter, we will discuss about rotational motion

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved