In the previous section, we saw the basics about moment of inertia. In this section we will see radius of gyration
■ In translational motion, we saw this:
• Inertia is a property of matter by which it continues in its existing state of rest or uniform motion in a straight line, unless that state is changed by an external force.
• Also, we saw that, mass is a measure of this inertia
■ Now, in rotational motion, we have not inertia, but moment of inertia
• Rotational inertia is the a property of matter by which it continues in its existing state of rest or uniform rotational motion about an axis, unless that state is changed by an external force.
• 'moment of inertia' is the measure of ‘rotational inertia’
• We want to know how this distribution is present in a body
• Moment of inertia helps us to acquire that information
• But always remember these:
♦ Mass of a body is a constant
♦ But moment of inertia of a body depends upon the axis that we choose
1. We know the formula for finding I
$\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• So, if mass is increased, I increases
• If the distances of the particles from the axis is increased, then also I increases
2. So large heavy discs will have a high I
• Because of this large I that they possess,
♦ If they are initially at rest, it will be difficult to get them rotating
♦ If they are initially in rotational motion, it will be difficult to stop them
3. Such large heavy discs are used in steam engines and automobile engines
• They are called flywheels
♦ Because of their large I, we will not be able to put the vehicle (which is initially at rest) into a sudden motion
♦ Also we will not be able to bring a vehicle (which is initially in motion) into a sudden stop
• This helps to prevent jerky motion of the vehicle so that the passengers can experience a smoother ride
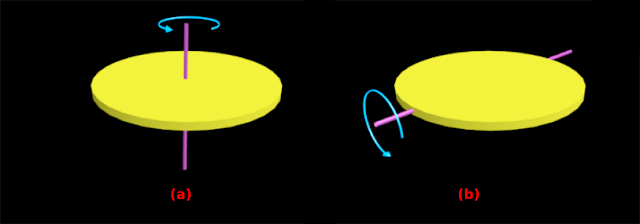
1. Body: Thin circular ring of radius R
Axis: Perpendicular to the plane of the ring, passing through the center
■ $\mathbf\small{I=MR^2}$
2. Body: Thin circular ring of radius R
Axis: Lies on the plane of the ring, passing through the center. Obviously, this axis is the extension of any one diameter of the ring
■ $\mathbf\small{I=\frac{MR^2}{2}}$
3. Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
■ $\mathbf\small{I=\frac{ML^2}{12}}$
4. Body: Circular disc of radius R
Axis: Perpendicular to the disc, passing through the center
■ $\mathbf\small{I=\frac{MR^2}{2}}$
5. Body: Circular disc of radius R
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
■ $\mathbf\small{I=\frac{MR^2}{4}}$
6. Body: Solid cylinder of radius R
Axis: Axis of the cylinder
■ $\mathbf\small{I=\frac{MR^2}{2}}$
7. Body: Hollow cylinder of radius R
Axis: Axis of the cylinder
■ $\mathbf\small{I=MR^2}$
8. Body: Solid sphere of radius R
Axis: Passes through the center. Obviously, this axis is the extension of any one diameter of the sphere
■ $\mathbf\small{I=\frac{2MR^2}{5}}$
1. We see that, in all case,
♦ Mass occurs once
♦ Length occurs twice
2. The dimensions of I is ML2
• The SI unit of I is: kg m2
3. So we can write I in another form:
I = Mk2.
♦ Where k is called the radius of gyration
♦ It has the dimension: L
4. Let us see an example:
(i) In case 3 above, we have: $\mathbf\small{I=\frac{ML^2}{12}}$
(ii) But I = Mk2
(iii) Equating the two, we get: $\mathbf\small{I=\frac{ML^2}{12}=Mk^2}$
$\mathbf\small{\Rightarrow k^2=\frac{L^2}{12}}$
$\mathbf\small{\Rightarrow k=\frac{L}{\sqrt{12}}}$
(iv) So for case 3, we can write:
Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
■ $\mathbf\small{I=\frac{ML^2}{12}}$
■ $\mathbf\small{k=\frac{L}{\sqrt{12}}}$
Note that, just like I, k also depends on the axis
5. Another example:
(i) In case 5 above, we have: $\mathbf\small{I=\frac{MR^2}{4}}$
(ii) But I = Mk2
(iii) Equating the two, we get: $\mathbf\small{I=\frac{MR^2}{4}=Mk^2}$
$\mathbf\small{\Rightarrow \frac{R^2}{4}=k^2}$
$\mathbf\small{\Rightarrow k=\frac{R}{2}}$
(iv) So for case 5, we can write:
Body: Circular disc of radius R
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
■ $\mathbf\small{I=\frac{MR^2}{4}}$
■ $\mathbf\small{k=\frac{R}{2}}$
6. We know that, I of a body is given by: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• It is clear that, we have to consider each one of the n particles in the body
♦ We want the mass of each particle
♦ We want the perpendicular distance of each particle from the axis
7. But if the body consists of only one particle, then the I of that body is given by:
$\mathbf\small{I={m\;r_{(\bot)}^2}}$
• I of this body can be obtained using it's k also:
$\mathbf\small{I={m\;k^2}}$
• So, for this body, we get:
$\mathbf\small{I={m\;r_{(\bot)}^2}={m\;k^2}}$
8. Based on the above analysis, we can write the following:
(i) Let a body 'A' of mass M, contain n particles
(ii) Let it's moment of inertia about an axis 'L' be I
(iii) Let it's radius of gyration about 'L' be k
• Then we get: $\mathbf\small{I={M\;k^2}}$
(iv) Now consider a point mass 'B'. See fig.7.116 below
• Let the mass of 'B' be the same 'M' possessed by A
(v) Place 'B' at a perpendicular distance of 'k' from the axis 'L'
• Then moment of inertia of B about 'L' = $\mathbf\small{{M\;k^2}}$
• This is the same I possessed by the body 'A'
9. So we can write the definition of k of a body A about an axis L:
The definition can be written in 4 steps:
(i) Take a point mass B such that:
• It's mass is equal to the mass of A
(ii) We want B to have the same I (about L) possessed by A
(iii) For that, we must place B at a 'particular perpendicular distance' from L
(iv) This 'particular perpendicular distance' is k
This is shown in fig.7.116 below:
■ In translational motion, we saw this:
• Inertia is a property of matter by which it continues in its existing state of rest or uniform motion in a straight line, unless that state is changed by an external force.
• Also, we saw that, mass is a measure of this inertia
■ Now, in rotational motion, we have not inertia, but moment of inertia
• Rotational inertia is the a property of matter by which it continues in its existing state of rest or uniform rotational motion about an axis, unless that state is changed by an external force.
• 'moment of inertia' is the measure of ‘rotational inertia’
• Different parts of a body are distributed at different distances from the axis
• Moment of inertia helps us to acquire that information
• But always remember these:
♦ Mass of a body is a constant
♦ But moment of inertia of a body depends upon the axis that we choose
Let us see a practical application of moment of inertia. We will write it in steps:
$\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• So, if mass is increased, I increases
• If the distances of the particles from the axis is increased, then also I increases
2. So large heavy discs will have a high I
• Because of this large I that they possess,
♦ If they are initially at rest, it will be difficult to get them rotating
♦ If they are initially in rotational motion, it will be difficult to stop them
3. Such large heavy discs are used in steam engines and automobile engines
• They are called flywheels
♦ Because of their large I, we will not be able to put the vehicle (which is initially at rest) into a sudden motion
♦ Also we will not be able to bring a vehicle (which is initially in motion) into a sudden stop
• This helps to prevent jerky motion of the vehicle so that the passengers can experience a smoother ride
We saw the I of 8 objects in the previous section. We will write them again here:
Axis: Perpendicular to the plane of the ring, passing through the center
■ $\mathbf\small{I=MR^2}$
2. Body: Thin circular ring of radius R
Axis: Lies on the plane of the ring, passing through the center. Obviously, this axis is the extension of any one diameter of the ring
■ $\mathbf\small{I=\frac{MR^2}{2}}$
3. Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
■ $\mathbf\small{I=\frac{ML^2}{12}}$
4. Body: Circular disc of radius R
Axis: Perpendicular to the disc, passing through the center
■ $\mathbf\small{I=\frac{MR^2}{2}}$
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
■ $\mathbf\small{I=\frac{MR^2}{4}}$
6. Body: Solid cylinder of radius R
Axis: Axis of the cylinder
■ $\mathbf\small{I=\frac{MR^2}{2}}$
Axis: Axis of the cylinder
■ $\mathbf\small{I=MR^2}$
8. Body: Solid sphere of radius R
Axis: Passes through the center. Obviously, this axis is the extension of any one diameter of the sphere
■ $\mathbf\small{I=\frac{2MR^2}{5}}$
Based on the above results we can write an analysis. We will write it in steps:
♦ Mass occurs once
♦ Length occurs twice
2. The dimensions of I is ML2
• The SI unit of I is: kg m2
3. So we can write I in another form:
I = Mk2.
♦ Where k is called the radius of gyration
♦ It has the dimension: L
4. Let us see an example:
(i) In case 3 above, we have: $\mathbf\small{I=\frac{ML^2}{12}}$
(ii) But I = Mk2
(iii) Equating the two, we get: $\mathbf\small{I=\frac{ML^2}{12}=Mk^2}$
$\mathbf\small{\Rightarrow k^2=\frac{L^2}{12}}$
$\mathbf\small{\Rightarrow k=\frac{L}{\sqrt{12}}}$
(iv) So for case 3, we can write:
Body: Thin rod of length L
Axis: Perpendicular to the rod, passing through the midpoint
■ $\mathbf\small{I=\frac{ML^2}{12}}$
■ $\mathbf\small{k=\frac{L}{\sqrt{12}}}$
Note that, just like I, k also depends on the axis
5. Another example:
(i) In case 5 above, we have: $\mathbf\small{I=\frac{MR^2}{4}}$
(ii) But I = Mk2
(iii) Equating the two, we get: $\mathbf\small{I=\frac{MR^2}{4}=Mk^2}$
$\mathbf\small{\Rightarrow \frac{R^2}{4}=k^2}$
$\mathbf\small{\Rightarrow k=\frac{R}{2}}$
(iv) So for case 5, we can write:
Body: Circular disc of radius R
Axis: Lies on the plane of the disc, passing through the center. Obviously, this axis is the extension of any one diameter of the disc
■ $\mathbf\small{I=\frac{MR^2}{4}}$
■ $\mathbf\small{k=\frac{R}{2}}$
6. We know that, I of a body is given by: $\mathbf\small{I=\sum\limits_{i=1}^{i=n}{\left(m_i\;r_{i(\bot)}^2 \right)} }$
• It is clear that, we have to consider each one of the n particles in the body
♦ We want the mass of each particle
♦ We want the perpendicular distance of each particle from the axis
7. But if the body consists of only one particle, then the I of that body is given by:
$\mathbf\small{I={m\;r_{(\bot)}^2}}$
• I of this body can be obtained using it's k also:
$\mathbf\small{I={m\;k^2}}$
• So, for this body, we get:
$\mathbf\small{I={m\;r_{(\bot)}^2}={m\;k^2}}$
8. Based on the above analysis, we can write the following:
(i) Let a body 'A' of mass M, contain n particles
(ii) Let it's moment of inertia about an axis 'L' be I
(iii) Let it's radius of gyration about 'L' be k
• Then we get: $\mathbf\small{I={M\;k^2}}$
(iv) Now consider a point mass 'B'. See fig.7.116 below
• Let the mass of 'B' be the same 'M' possessed by A
(v) Place 'B' at a perpendicular distance of 'k' from the axis 'L'
• Then moment of inertia of B about 'L' = $\mathbf\small{{M\;k^2}}$
• This is the same I possessed by the body 'A'
9. So we can write the definition of k of a body A about an axis L:
The definition can be written in 4 steps:
(i) Take a point mass B such that:
• It's mass is equal to the mass of A
(ii) We want B to have the same I (about L) possessed by A
(iii) For that, we must place B at a 'particular perpendicular distance' from L
(iv) This 'particular perpendicular distance' is k
This is shown in fig.7.116 below:
 |
| Fig.7.116 |
In the next section, we will see theorem of perpendicular axes