In the previous section we saw the equations related to projectile motion. In this section, we will see how those equations are applied to an actual projectile.
■ An object is projected with a velocity of 30 ms-1 at an angle of 60o with the horizontal. Write all the details regarding it's motion. [g = 9.81 ms-2]
Solution:
We have the following data:
• Magnitude of Initial velocity $\mathbf\small{\left | \vec{v_0} \right |}$ = 30 ms-1
• Angle of initial velocity θ0 = 60o.
We can calculate the following 5 items:
1. Path of the projectile:
• It is given by the equation of the parabola (Eq.4.15): $\mathbf\small{y=\left [ \tan\theta_0 \right ]x-\left [ \frac{g}{2\left ( \left | \vec{v_0} \right |\cos \theta_0 \right )^2} \right ]x^2}$
• Substituting the values, we get: $\mathbf\small{y=1.7321x-0.0218x^2}$
• The parabola is plotted in fig.4.30 below:
2. Time required to reach the maximum height:
• We can use Eq.4.16: $\mathbf\small{t_m=\frac{\left | \vec{v_0} \right |\sin \theta_0}{g}}$
• Substituting the values, we get: tm = 2.648 s
3. Maximum height reached by the projectile:
• We can use Eq.4.17: $\mathbf\small{h_m=\frac{\left (\left | \vec v_0 \right| \sin \theta_0 \right )^2}{2g}}$
• Substituting the values, we get: hm = 34.4037 m
■ So the height is nearly 35 m. In fig.4.30 above, we see that, the peak point is close to the horizontal line through 35 m
4. Time required for the whole flight:
• We can use Eq.4.18: $\mathbf\small{T_f=\frac{2\left | \vec{v_0} \right |\sin \theta_0}{g}}$
• Substituting the values, we get: Tf = 5.297 s
5. Horizontal range:
• We can use Eq.4.19: $\mathbf\small{\left |\vec{R} \right |=\frac{\left ( \left | \vec{v_0} \right |^2 \sin 2\theta_0 \right )}{g}}$
• Substituting the values, we get: R = 79.45 m
■So the range is nearly 80 m. In fig.4.30 above, we see that, the path meets the x axis at a point which is close to 80 m
Based on the above example, we will now see some interesting features which are applicable to all such projectiles
6. The fig.4.31 below shows the same projectile path that we saw in fig.4.30
• Draw a line parallel to the x axis.
♦ It can be at any height above zero
♦ It can be at any height below the maximum height which is 34.4 m
• That is., 0 < Height of the horizontal line < 34.4
• Such a line is shown in magenta colour.
7. The height of this magenta line is 22 m. It cuts the path at two points P and P'
■ So it is clear: The object is at a vertical distance of 22 m from the ground twice during it's journey
• First time: When at P, it is at a vertical distance of 22 m from the ground
• Second time: When at P', it is at a vertical distance of 22 m from the ground
8. Let us find the resultant velocity of the object at those two points
A. First we will consider P
• We want the horizontal velocity $\mathbf\small{\vec{v_x}}$ at P
• We want the vertical velocity $\mathbf\small{\vec{v_y}}$ at P
• We want the resultant $\mathbf\small{\vec{v}}$ of the two
■ For that, we do the following steps (i) to (viii):
(i) Starting from the origin, what time is required to reach P?
• For finding that time, we first need to find the horizontal distance of P from the origin O
• This can be found out by putting 'y = 22' in the equation of the parabola (see (1) above)
We get: 22 = 1.7321 x - 0.0218 x2.
(ii) This is a quadratic equation in x. Solving it, we get:
x = 15.872 and x = 63.582 m
(iii) We get 2 values for x. It is obvious because, the object is '22 m vertically away' at the two instances P and P'
♦ The lesser value x = 15.872 corresponds to P
♦ The greater value x = 63.582 corresponds to P'
• So P is 15.872 m 'horizontally away' from O
(iv) We know that the horizontal velocity is always the same:
• It's magnitude is given by: $\mathbf\small{\left | \vec{v_x} \right |=\left | \vec{v}\right |\cos \theta_0}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_x} \right |}$ = 15 ms-1.
• It's direction is towards positive side of the x axis
■ We can write:
The object traveled 15.872 m horizontally with a velocity of 15 ms-1 for a duration of 't' s to reach P
• Thus we get: 15 × t = 15.872
• So t = 1.058 s
(v) During this 1.058 s, it traveled vertically also.
• But this vertical travel was not with a constant velocity. Because, the vertical travel is affected by '-g'. We can write:
♦ This vertical travel has an initial velocity of v0sin θ0
♦ This vertical travel has a duration of 1.058 s
♦ This vertical travel has an acceleration of -g
(vi) We can use the familiar equation: v = v0 + at
• We get: $\mathbf\small{\left | \vec{v_y} \right |=\left | \vec{v_{0y}} \right |-gt}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_y} \right |}$ = (30 sin 60) - (9.81 × 1.058) = 15.602 ms-1.
• It's direction is towards positive side of the y axis
(vii) Now we can find the resultant velocity:
• Magnitude of the resultant = $\mathbf\small{\left | \vec{v} \right |=\sqrt{\left | \vec{v_x} \right |^2+\left | \vec{v_y} \right |^2}}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v} \right |}$ = √[152 + 15.6022] = 21.643 ms-1.
(vii) Direction of this velocity is given by: $\mathbf\small{\tan \theta=\frac{\left | \vec{v_y} \right |}{\left | \vec{v_x} \right |}=\frac{15.602}{15}=1.04}$
• So θ = tan-1 (1.04) = 46.127o.
(viii) We can write:
• The resultant velocity $\mathbf\small{\vec{v}}$ at P has a magnitude of 21.643 ms-1
• It has a direction which makes 46.127o with the x axis
This is shown in fig.4.32 below:
B. Now we will take up P'
• We want the horizontal velocity $\mathbf\small{\vec{v_x}}$ at P'
• We want the vertical velocity $\mathbf\small{\vec{v_y}}$ at P'
• We want the resultant $\mathbf\small{\vec{v}}$ of the two
■ For that, we do the following steps (i) to (viii):
(i) Starting from the origin, what time is required to reach P'?
• For finding that time, we first need to find the horizontal distance of P' from the origin O
• We already obtained it as 63.582 m
(ii) We know that, the horizontal velocity is always the same. We obtained it as 15 ms-1.
• It's direction is towards the positive side of the x axis
• We can write:
• Starting from O, the object travelled 63.582 m horizontally with a velocity of 15 ms-1 for a duration of 't' s to reach P
• Thus we get: 15 × t = 63.587
• So t = 4.239 s
(iii) The object first reached the highest point M within 2.648 s (See (2) above)
• Then it fell downwards to reach P'
• So the time to fall from M to P' = (4.239 - 2.648) = 1.591 s
(iv) Now consider the vertical travel from M to P':
• This vertical travel has an initial velocity of 0 ms-1.
• This vertical travel has a duration of 1.591 s
• This vertical travel has an acceleration of g
(v) We can use the familiar equation: v = v0 + at
• We get: $\mathbf\small{\left | \vec{v_y} \right |=\left | \vec{v_{0y}} \right |+gt}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_y} \right |}$ = (0) + (9.81 × 1.591) = 15.607 ms-1.
• It's direction is towards negative side of the y axis
(vi) Now we can find the resultant velocity:
• Magnitude of the resultant = $\mathbf\small{\left | \vec{v} \right |=\sqrt{\left | \vec{v_x} \right |^2+\left | \vec{v_y} \right |^2}}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v} \right |}$ = √[152 + 15.6072] = 21.647 ms-1.
(vii) Direction of this velocity is given by: $\mathbf\small{\tan \theta=\frac{\left | \vec{v_y} \right |}{\left | \vec{v_x} \right |}=\frac{15.608}{15}=1.04}$
• So θ = tan-1 (1.04) = 46.13o.
(viii) We can write:
• The resultant velocity $\mathbf\small{\vec{v}}$ at P' has a magnitude of 21.647 ms-1
• It has a direction which makes 46.13o with the x axis
• This is shown in the fig.4.32 above
9. Note that, P and P' are symmetric points
■ The resultant velocity at both P and P' have the same magnitudes
■ The direction θ are also same at P and P'. But ..
• At P, θ is above the horizontal
• At P', θ is below the horizontal
10. Like P and P', the following two points are also symmetric:
• Point of origin of the flight
• Point where the projectile returns to the x axis
■ So we get:
The following two magnitudes will be the same:
• $\mathbf\small{|\vec{v_0}|}$ at the origin
• $\mathbf\small{|\vec{v}|}$ at the point where the projectile returns to the x axis
■ Also, the following two angles will be equal:
• θ0 at the origin
• θ at the point where the projectile returns to the x axis
But..
♦ θ0 is above the horizontal
♦ θ is above the horizontal
11. We derived the results in (10) by using symmetry. The reader may prove them by finding the actual velocity at the point where the projectile returns to the x axis
10. Now we will see an interesting point about the times at P and P'
(i) we saw that, time required to reach P is 1.048 s. See 8A(iv) above.
(ii) we saw that, time required to reach P' is 4.239 s. See 8B(ii) above.
(iii) We have also calculated Tf as 5.297 s. See (4) above.
• So the time required to travel from P to the 'end point of the flight' = (5.297-4.239) = 1.058 s. This is same as (i)
■ We can write: P and P' are two symmetric points
• The following two times are equal:
♦ The time required to reach P from 'origin of the flight'
♦ The time required to reach the 'end of the flight' from P'
■ The above result can be related to the fact that another set of two times are also equal:
♦ The time required to reach M from 'origin of the flight'
♦ The time required to reach the 'end of the flight' from M
■ An object is projected with a velocity of 30 ms-1 at an angle of 60o with the horizontal. Write all the details regarding it's motion. [g = 9.81 ms-2]
Solution:
We have the following data:
• Magnitude of Initial velocity $\mathbf\small{\left | \vec{v_0} \right |}$ = 30 ms-1
• Angle of initial velocity θ0 = 60o.
We can calculate the following 5 items:
1. Path of the projectile:
• It is given by the equation of the parabola (Eq.4.15): $\mathbf\small{y=\left [ \tan\theta_0 \right ]x-\left [ \frac{g}{2\left ( \left | \vec{v_0} \right |\cos \theta_0 \right )^2} \right ]x^2}$
• Substituting the values, we get: $\mathbf\small{y=1.7321x-0.0218x^2}$
• The parabola is plotted in fig.4.30 below:
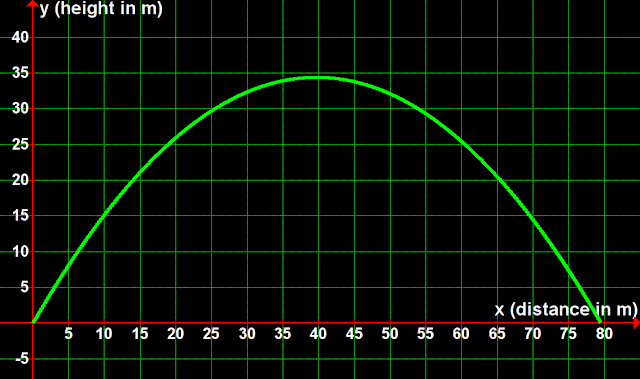 |
| Fig.4.30 |
• We can use Eq.4.16: $\mathbf\small{t_m=\frac{\left | \vec{v_0} \right |\sin \theta_0}{g}}$
• Substituting the values, we get: tm = 2.648 s
3. Maximum height reached by the projectile:
• We can use Eq.4.17: $\mathbf\small{h_m=\frac{\left (\left | \vec v_0 \right| \sin \theta_0 \right )^2}{2g}}$
• Substituting the values, we get: hm = 34.4037 m
■ So the height is nearly 35 m. In fig.4.30 above, we see that, the peak point is close to the horizontal line through 35 m
4. Time required for the whole flight:
• We can use Eq.4.18: $\mathbf\small{T_f=\frac{2\left | \vec{v_0} \right |\sin \theta_0}{g}}$
• Substituting the values, we get: Tf = 5.297 s
5. Horizontal range:
• We can use Eq.4.19: $\mathbf\small{\left |\vec{R} \right |=\frac{\left ( \left | \vec{v_0} \right |^2 \sin 2\theta_0 \right )}{g}}$
• Substituting the values, we get: R = 79.45 m
■So the range is nearly 80 m. In fig.4.30 above, we see that, the path meets the x axis at a point which is close to 80 m
Based on the above example, we will now see some interesting features which are applicable to all such projectiles
6. The fig.4.31 below shows the same projectile path that we saw in fig.4.30
 |
| Fig.4.31 |
♦ It can be at any height above zero
♦ It can be at any height below the maximum height which is 34.4 m
• That is., 0 < Height of the horizontal line < 34.4
• Such a line is shown in magenta colour.
7. The height of this magenta line is 22 m. It cuts the path at two points P and P'
■ So it is clear: The object is at a vertical distance of 22 m from the ground twice during it's journey
• First time: When at P, it is at a vertical distance of 22 m from the ground
• Second time: When at P', it is at a vertical distance of 22 m from the ground
8. Let us find the resultant velocity of the object at those two points
A. First we will consider P
• We want the horizontal velocity $\mathbf\small{\vec{v_x}}$ at P
• We want the vertical velocity $\mathbf\small{\vec{v_y}}$ at P
• We want the resultant $\mathbf\small{\vec{v}}$ of the two
■ For that, we do the following steps (i) to (viii):
(i) Starting from the origin, what time is required to reach P?
• For finding that time, we first need to find the horizontal distance of P from the origin O
• This can be found out by putting 'y = 22' in the equation of the parabola (see (1) above)
We get: 22 = 1.7321 x - 0.0218 x2.
(ii) This is a quadratic equation in x. Solving it, we get:
x = 15.872 and x = 63.582 m
(iii) We get 2 values for x. It is obvious because, the object is '22 m vertically away' at the two instances P and P'
♦ The lesser value x = 15.872 corresponds to P
♦ The greater value x = 63.582 corresponds to P'
• So P is 15.872 m 'horizontally away' from O
(iv) We know that the horizontal velocity is always the same:
• It's magnitude is given by: $\mathbf\small{\left | \vec{v_x} \right |=\left | \vec{v}\right |\cos \theta_0}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_x} \right |}$ = 15 ms-1.
• It's direction is towards positive side of the x axis
■ We can write:
The object traveled 15.872 m horizontally with a velocity of 15 ms-1 for a duration of 't' s to reach P
• Thus we get: 15 × t = 15.872
• So t = 1.058 s
(v) During this 1.058 s, it traveled vertically also.
• But this vertical travel was not with a constant velocity. Because, the vertical travel is affected by '-g'. We can write:
♦ This vertical travel has an initial velocity of v0sin θ0
♦ This vertical travel has a duration of 1.058 s
♦ This vertical travel has an acceleration of -g
(vi) We can use the familiar equation: v = v0 + at
• We get: $\mathbf\small{\left | \vec{v_y} \right |=\left | \vec{v_{0y}} \right |-gt}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_y} \right |}$ = (30 sin 60) - (9.81 × 1.058) = 15.602 ms-1.
• It's direction is towards positive side of the y axis
(vii) Now we can find the resultant velocity:
• Magnitude of the resultant = $\mathbf\small{\left | \vec{v} \right |=\sqrt{\left | \vec{v_x} \right |^2+\left | \vec{v_y} \right |^2}}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v} \right |}$ = √[152 + 15.6022] = 21.643 ms-1.
(vii) Direction of this velocity is given by: $\mathbf\small{\tan \theta=\frac{\left | \vec{v_y} \right |}{\left | \vec{v_x} \right |}=\frac{15.602}{15}=1.04}$
• So θ = tan-1 (1.04) = 46.127o.
(viii) We can write:
• The resultant velocity $\mathbf\small{\vec{v}}$ at P has a magnitude of 21.643 ms-1
• It has a direction which makes 46.127o with the x axis
This is shown in fig.4.32 below:
 |
| Fig.4.32 |
• We want the horizontal velocity $\mathbf\small{\vec{v_x}}$ at P'
• We want the vertical velocity $\mathbf\small{\vec{v_y}}$ at P'
• We want the resultant $\mathbf\small{\vec{v}}$ of the two
■ For that, we do the following steps (i) to (viii):
(i) Starting from the origin, what time is required to reach P'?
• For finding that time, we first need to find the horizontal distance of P' from the origin O
• We already obtained it as 63.582 m
(ii) We know that, the horizontal velocity is always the same. We obtained it as 15 ms-1.
• It's direction is towards the positive side of the x axis
• We can write:
• Starting from O, the object travelled 63.582 m horizontally with a velocity of 15 ms-1 for a duration of 't' s to reach P
• Thus we get: 15 × t = 63.587
• So t = 4.239 s
(iii) The object first reached the highest point M within 2.648 s (See (2) above)
• Then it fell downwards to reach P'
• So the time to fall from M to P' = (4.239 - 2.648) = 1.591 s
(iv) Now consider the vertical travel from M to P':
• This vertical travel has an initial velocity of 0 ms-1.
• This vertical travel has a duration of 1.591 s
• This vertical travel has an acceleration of g
(v) We can use the familiar equation: v = v0 + at
• We get: $\mathbf\small{\left | \vec{v_y} \right |=\left | \vec{v_{0y}} \right |+gt}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v_y} \right |}$ = (0) + (9.81 × 1.591) = 15.607 ms-1.
• It's direction is towards negative side of the y axis
(vi) Now we can find the resultant velocity:
• Magnitude of the resultant = $\mathbf\small{\left | \vec{v} \right |=\sqrt{\left | \vec{v_x} \right |^2+\left | \vec{v_y} \right |^2}}$
• Substituting the values, we get: $\mathbf\small{\left | \vec{v} \right |}$ = √[152 + 15.6072] = 21.647 ms-1.
(vii) Direction of this velocity is given by: $\mathbf\small{\tan \theta=\frac{\left | \vec{v_y} \right |}{\left | \vec{v_x} \right |}=\frac{15.608}{15}=1.04}$
• So θ = tan-1 (1.04) = 46.13o.
(viii) We can write:
• The resultant velocity $\mathbf\small{\vec{v}}$ at P' has a magnitude of 21.647 ms-1
• It has a direction which makes 46.13o with the x axis
• This is shown in the fig.4.32 above
9. Note that, P and P' are symmetric points
■ The resultant velocity at both P and P' have the same magnitudes
■ The direction θ are also same at P and P'. But ..
• At P, θ is above the horizontal
• At P', θ is below the horizontal
10. Like P and P', the following two points are also symmetric:
• Point of origin of the flight
• Point where the projectile returns to the x axis
■ So we get:
The following two magnitudes will be the same:
• $\mathbf\small{|\vec{v_0}|}$ at the origin
• $\mathbf\small{|\vec{v}|}$ at the point where the projectile returns to the x axis
■ Also, the following two angles will be equal:
• θ0 at the origin
• θ at the point where the projectile returns to the x axis
But..
♦ θ0 is above the horizontal
♦ θ is above the horizontal
11. We derived the results in (10) by using symmetry. The reader may prove them by finding the actual velocity at the point where the projectile returns to the x axis
10. Now we will see an interesting point about the times at P and P'
(i) we saw that, time required to reach P is 1.048 s. See 8A(iv) above.
(ii) we saw that, time required to reach P' is 4.239 s. See 8B(ii) above.
(iii) We have also calculated Tf as 5.297 s. See (4) above.
• So the time required to travel from P to the 'end point of the flight' = (5.297-4.239) = 1.058 s. This is same as (i)
■ We can write: P and P' are two symmetric points
• The following two times are equal:
♦ The time required to reach P from 'origin of the flight'
♦ The time required to reach the 'end of the flight' from P'
■ The above result can be related to the fact that another set of two times are also equal:
♦ The time required to reach M from 'origin of the flight'
♦ The time required to reach the 'end of the flight' from M
In the next section, we will see some solved examples.
Copyright©2018 Higher Secondary Physics. blogspot.in - All Rights Reserved
No comments:
Post a Comment