In the previous section we saw the basics about thermal expansion. We saw the details about coefficients of linear, area and volume expansion. In this section we will see a few more details.
Let us see whether the coefficients have constant values or not. It can be analyzed in 3 steps:
1. Consider the coefficient of linear expansion (𝛼L)
• Each material has it's own definite value of 𝛼L
• In other words, the 𝛼L value of a material will be constant
2. This can be explained using an example. It can be written in 3 steps:
(i) We want to find the increase in length when a 50 cm long iron rod is heated from 60 to 70 oC
• We can easily calculate it using Eq.11.1: Δl=𝛼L l Δt
♦ We get: Δl=500 𝛼L
(ii) Next we want to find the increase in length of the same rod when it is heated from 80 to 95 oC
• We use the same Eq.11.1
♦ We get: Δl=750 𝛼L
(iii) We will be using the same value of 𝛼L in both (i) and (ii)
■ In general, a substance will have a constant value for 𝛼L.
3. But when we calculate volume expansions, there is a difficulty
• This can be explained using an example. It can be written in 3 steps:
(i) We want to find the increase in volume when a 50 cm3 block of iron is heated from 60 to 70 oC
• We can easily calculate it using Eq.11.3: ΔV=𝛼V V Δt
♦ We get: ΔV=500 𝛼V
(ii) Next we want to find the increase in volume of the same block when it is heated from 80 to 95 oC
• We use the same Eq.11.3
♦ We get: ΔV=750 𝛼V
(iii) Here, we cannot use the same value of 𝛼V in both (i) and (ii)
• There will be a small difference
■ This is because, 𝛼V of most substances depend on temperature. They become constant only at high temperatures
It can be written in 5 steps:
1. Fig.11.2(a) below, shows a metal plate with a circular plug in the middle
• The plate and the plug are made of the same metal
• The plug has a perfect fit in the circular hole of the plate
 |
| Fig.11.2 |
2. When we heat the plate and the plug together, both will expand to a higher volume. This is shown in fig.b
• In the expanded situation also, the plug will have the perfect fit in the hole
■ That means, the plug and the hole suffer the same amount of thermal expansion
3. In our present case, the plug and hole are circular
• But the result in (2) is valid even when the plug and hole has other shapes like square, rectangular, triangular etc.,
4. Also, the result in (2) can be written in terms of diameter:
♦ The increase in diameter of the plug
♦ is equal to
♦ The increase in diameter of the hole
5. Now imagine that, the plate is heated without the plug
• Then also, the diameter of the hole will increase
• This is shown in figs.11.3(a) and (b) below:
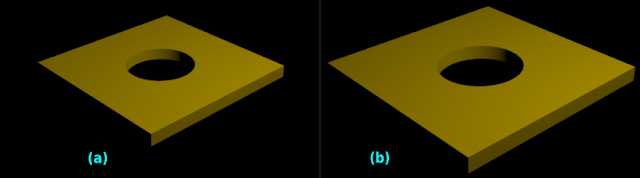 |
| Fig.11.3 |
First we will see the relation between 𝛼L and 𝛼V. It can be written in 6 steps:
1. Consider a cube with length of side l
• When it is heated, the length of side becomes (l+Δl)
2. So the new volume will be: (l+Δl)3
• This can be expanded using the identity:
(a+b)3 = a3 + 3a2b + 3ab2 + b3
• So we get:
(l+Δl)3 = l3 + 3 l2 Δl + 3 l Δl2 + Δl3
3. Δl is small compared to l
♦ So Δl2 and Δl3 will be very small
♦ So we can ignore the square terms and cubic terms of Δl
♦ Thus the new volume will be: (l3 + 3 l2 Δl)
4. So the increase in volume, ΔV = [(l3 + 3 l2 Δl) - l3] = 3 l2 Δl
• Multiplying numerator and denominator of the right side by l, we get:
$\mathbf\small{\rm{\Delta V = \frac{3l^3 \Delta l}{l}}}$
⇒ $\mathbf\small{\rm{\Delta V = \frac{3V \Delta l}{l}}}$
5. But from Eq.11.1, we have: $\mathbf\small{\rm{\frac{\Delta l}{l}=\alpha_L\, \Delta t}}$
• So the result in (4) becomes: $\mathbf\small{\rm{\Delta V = 3V \alpha_L \Delta t}}$
6. But from Eq.11.3, we have: $\mathbf\small{\rm{\frac{\Delta V}{V}=\alpha_V\, \Delta t}}$
• So the result in (5) becomes: 𝛼V Δt = 3 𝛼L Δt
• Thus we get Eq.11.4: 𝛼V = 3 𝛼L
1. Consider a rectangular plate of length a and width b
2. When heated,
♦ it's length increases by Δa and becomes (a+Δa)
♦ it's width increases Δb by and becomes (b+Δb)
3. So the final area is: [(a+Δa)(b+Δb)]
• Expanding this, we get: Final area = [ab+Δa b+a Δb+Δa Δb]
• So increase in area, ΔA = [ab+Δa b+a Δb+Δa Δb] - ab = [Δa b+a Δb+Δa Δb]
4. Using Eq.11.1, we have:
♦ Δa = 𝛼L a Δt
♦ Δb = 𝛼L b Δt
5. Consider the result in (3)
• The last term involves the product of Δa and Δb
• This product can be obtained from (4): [Δa Δb] = [(𝛼L a Δt)(𝛼L b Δt)]
• 𝛼L is a small quantity of the order 10-5. So (𝛼L×𝛼L) will be very small. We can ignore that term
6. So the result in (3) becomes:
ΔA = [Δa b+a Δb]
• Using the results in (4), this becomes:
ΔA = [(𝛼L a Δt)b + (𝛼L b Δt)a] = [2 𝛼L ab Δt] = [2 𝛼L A Δt]
7. But from Eq.11.2, we have: ΔA = [𝛼A A Δt]
• Equating this to the result in (6), we get: [𝛼A A Δt] = [2 𝛼L A Δt]
• Thus we get Eq.11.5: 𝛼A = 2 𝛼L
Now we will see some solved examples
Solved example 11.1
Original height of a steel statue is 30 m. This height is measured when the temperature is 35 oC. What will be the height when the temperature falls to -5 oC?
𝛼L for steel = 1.2 × 10-5 k-1.
Solution:
1. We have Eq.11.1: ΔL = 𝛼L l Δt
2. Given that 𝛼L = 1.2 × 10-5 K-1
• Also Δt = [35- (-5)] = 40 oC
3. Substituting the known values in (1), we get:
ΔL = (2.5 × 10-6 × 30 × 40) = 0.0144 m
4. So height at -5 oC = (30-0.0144) = 29.98 m
5. Note that, the unit of is K-1
• But in this problem, we used oC for the temperatures
• This will not affect the result because, oC and K has the same 'unit size'
• In other words,
♦ The heat required to raise the temperature by 1 oC
♦ is same as
♦ The heat required to raise the temperature by 1 K
Solved example 11.2
Two wooden pegs are driven into the ground. The distance between them is 15 m when measured with a steel tape at 20 oC. What would be the reading when the distance is measured with the steel tape at 37 oC ?
Solution:
1. The wooden pegs A and B are shown in yellow color in fig.11.4 below:
 |
| Fig.11.4 |
• Whatever be the surrounding temperature, the distance between the pegs does not change
♦ This is because, the ground does not suffer any linear expansion
2. The steel tape at 20 oC shows 15 m reading
3. But when the temperature increase to 37 oC, the steel tape will increase in length
• The zero of the tape will be at A at all temperatures
• But due to the expansion, the '15 m mark' will move to the right beyond B
• So the reading at B will be less than 15 m
4. We want to know the 'distance moved by the 15 m mark'
• Obviously, it will be equal to the 'linear expansion (Δl) of a steel rod of 15 m length'
5. We have Eq.11.1: Δl = 𝛼L l Δt
• Substituting the known values, we get: Δl = (1.2 × 10-5 × 15 × 17) = 0.00306 m
• So new reading at B = (15-0.00306) = 14.997 m
Solved examples 11.3 to 11.7
In the next section, we will see some problems in volume expansion. We will also see anomalous behaviour of water and thermal stress
PREVIOUS
CONTENTS
NEXT
Copyright©2020 Higher Secondary Physics. blogspot.in - All Rights Reserved
No comments:
Post a Comment