Chapter 10.5 - Pascal's law

In the previous section, we saw the details about mercury barometer. In this section, we will see Pascal's law

Pascal's law can be explained in 7 steps:

1. Consider the arrangement shown in fig.10.22 below:

Fig.10.22

• A horizontal cylinder is shown in pink color

• It has a piston on it’s left end

2. Three vertical cylinders having different diameters are taken out from the horizontal cylinder

• We know that, though the vertical cylinders have different diameters, the liquid levels will be the same (in our present case, it is h₁)

• The pressure in the horizontal cylinder will be equal to 𝛒gh₁

    ♦ Where 𝛒 is the density of the liquid in the cylinder

• So initial pressure at the bottom of each vertical cylinder will be the same: 𝛒gh₁

3. Now, push the piston towards the right

• The pressure in the horizontal cylinder will increase

• The liquid will rise to a new ‘common level’ in all the vertical cylinders 

4. Note that: A new ‘common level’ (h₂) is attained

■ That means, the ‘increase in pressure’ in the horizontal cylinder is distributed equally among the vertical cylinders

    ♦ Each cylinder gets the same 'extra pressure'

    ♦ So the final pressure in each cylinder will be the same: 𝛒gh₂

■ Pascal’s law of transmission of fluid pressure states that:

Whenever external pressure is applied on any part of a fluid in a container, it is transmitted undiminished and equally in all directions

5. A simple demonstration of the law can be given using a filled balloon

• When we apply a force on any one portion of the balloon, the air inside will apply an outward force on every point of the balloon

• This is shown in fig.4.23 below:

Fig.10.23

6. The word 'undiminished' is used to indicate that, the 'applied external pressure' is completely available to act on every part of the fluid

    ♦ The distance between 'the point of application' to 'a far end of the fluid body' has no significance    

    ♦ If a pressure P is applied, both 'far ends' and 'near ends' will experience the same P

7. 'Equally in all directions' indicate that, the shape of the container has no significance

    ♦ The fluid may be contained inside a vessel of complicated shape

    ♦ Even then, if a pressure P is applied, all points of the fluid will experience the same P

The Hydraulic lift

• Working of the hydraulic lift is based on Pascal’s law. The details can be written in 5 steps:

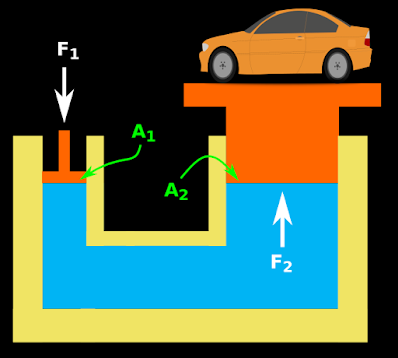
1. In fig.10.24, we see two pistons separated by a liquid

    ♦ The smaller piston has an area of A₁

    ♦ The larger piston has an area of A₂

Fig.10.24

2. A downward force F₁ is applied on the smaller piston

• Then the pressure experienced by the liquid will be $\mathbf\small{\rm{\frac{F_1}{A_1}}}$

3. According to Pascal’s law, this pressure will be experienced on the whole liquid body

• The liquid body will apply this pressure on the sides and roof of the container

■ So the larger piston will experience the same upward pressure $\mathbf\small{\rm{\frac{F_1}{A_1}}}$

4. Let F₂ be the upward force experienced by the larger piston

• Then the pressure experienced by the larger piston is equal to $\mathbf\small{\rm{\frac{F_2}{A_2}}}$

• This pressure is equal to $\mathbf\small{\rm{\frac{F_1}{A_1}}}$

5. So we can write: $\mathbf\small{\rm{\frac{F_1}{A_1}=\frac{F_2}{A_2}}}$

• From this we get: $\mathbf\small{\rm{F_2=\left(\frac{A_2}{A_1} \right )F_1}}$

• We see that: F₁ is multiplied by a factor $\mathbf\small{\rm{\frac{A_2}{A_1}}}$

    ♦ 'A₂ in the numerator' is larger than 'A₁ in the denominator'

    ♦ So the factor $\mathbf\small{\rm{\frac{A_2}{A_1}}}$ will be larger than 1

    ♦ So F₂ will be greater than F₁

■ That means, we can:

    ♦ lift a large load placed on the larger piston

    ♦ by applying a small force at the smaller piston

■ The factor $\mathbf\small{\rm{\frac{A_2}{A_1}}}$ is the mechanical advantage of the hydraulic lift

---

Solved example 10.12

Two syringes of different cross sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0 cm and 3.0 cm respectively. (a) Find the force exerted on the larger piston when a force of 10 N is applied to the smaller piston. (b) If the smaller piston is pushed in through 6.0 cm, how much does the larger piston move out?

Solution:

Part (a):

1. The arrangement is shown in fig.10.25(a) below:

Fig.10.25

• We have: $\mathbf\small{\rm{F_2=\left(\frac{A_2}{A_1} \right )F_1}}$

2. Substituting the known values, we get:

$\mathbf\small{\rm{F_2=\left(\frac{0.25 \times \pi \times 3^2}{0.25 \times \pi \times 1^2} \right )\times 10=90\;N}}$

Part (b):

1. Water is an incompressible liquid

• So all the volume which is pushed out from the left syringe will enter the right syringe

2.Volume pushed out from the left syringe will be (A₁ × 6)

• Let x be the distance moved by the piston of the right syringe. This is shown in fig.b

• So the volume entering the right syringe will be (A₂ × x)

3. Equating the two volumes, we get:

A₁ × 6 = A₂ × x

⇒ $\mathbf\small{\rm{x=\left(\frac{A_1}{A_2} \right )6}}$

4. Substituting the known values, we get: $\mathbf\small{\rm{x=\left(\frac{0.25 \times 1^2}{0.25 \times 3^2} \right )\times 6=0.67\;cm}}$

 

Solved example 10.13

In a car lift compressed air exerts a force F₁ on a small piston having a radius of 5.0 cm. This pressure is transmitted to a second piston of radius 15 cm (Fig 10.7). If the mass of the car to be lifted is 1350 kg, calculate F₁ . What is the pressure necessary to accomplish this task? (g = 9.8 ms^-2 ).

Solution:

Part (a):

1. We have: $\mathbf\small{\rm{F_1=\left(\frac{A_1}{A_2} \right )F_2}}$

2. Substituting the known values, we get:

$\mathbf\small{\rm{F_1=\left(\frac{0.25 \times 5^2}{0.25 \times 15^2} \right )\times 1350 \times 9.8=1470\;N}}$

Part (b):

1. We are applying a force of 1470 N on the small piston

2. The small piston has an area of (𝝅 × 5²) cm²

• So we are applying a pressure of:

$\mathbf\small{\rm{\frac{1470}{\pi \times 5^2}}}$ = 18.73 N cm^-2 = 1.873 × 10⁵ N m^-2

3. Normal atmospheric pressure at sea level is 1.013 × 10⁵ N m^-2

• So 1.873 × 10⁵ N m^-2 is nearly twice the atmospheric pressure    

Solved example 10.14

A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm². What maximum pressure would the smaller piston have to bear ?

Solution:

1. We have: $\mathbf\small{\rm{\frac{F_1}{A_1}=\frac{F_2}{A_2}}}$

2. Substituting the known values, we get: $\mathbf\small{\rm{\frac{F_1}{A_1}=\frac{3000 \times 9.8}{425 \times 10^{-4}}}}$ = 6.92 × 10⁵ Nm^-2

Hydraulic brake

• The working of the hydraulic brake system is also based on Pascal’s law. This can be explained in 4 steps:

1. When the driver apply a force on the brake pedal, he is actually pushing the piston of a ‘master cylinder’

2. The fluid inside this cylinder will move out and apply pressure on four other pistons

    ♦ These pistons are situated at the four wheels of the automobile

    ♦ These pistons have a larger area than the piston in the master cylinder

          ✰ So a small force is sufficient at the brake pedal

3. The large pistons press against the brake lining of the wheels

• Thus the wheels slow down and come to a stop

• A schematic diagram of the system can be seen here 

4. The advantage of this system can be explained in three steps:

(i) We know that:

• The pressure will be transmitted undiminished and equally in all directions

(ii) So all wheels will experience the same braking force

• Also all wheels will experience the braking force at the same time

(iii) This will enhance safety while applying brakes

---

In the next section, we will see buoyancy and flotation

PREVIOUS           CONTENTS          NEXT

Copyright©2020 Higher Secondary Physics. blogspot.in - All Rights Reserved