In the previous section, we saw the Universal law of Gravitation. We saw the method to calculate the magnitude of the force of attraction between two bodies. In this section we will see the details about the direction of that force
1. We have a force of attraction $\mathbf\small{|\vec{F}_G|}$ between two masses m1 and m2
• Consider the line joining the 'center of m1' and 'center of m2'
■ The $\mathbf\small{|\vec{F}_G|}$ will be acting along this line
• We need to fix up this line mathematically
• For that, we use vectors
2. Fig.8.10 below shows the two masses in 3D space
(i) $\mathbf\small{\vec{r}_1}$ is the position vector of m1
• If we have $\mathbf\small{\vec{r}_1}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m1 in 3D space (Details here)
(ii) $\mathbf\small{\vec{r}_2}$ is the position vector of m2
• If we have $\mathbf\small{\vec{r}_2}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m2 in 3D space
3. Subtract $\mathbf\small{\vec{r}_2}$ from $\mathbf\small{\vec{r}_1}$
• Remember that, it should be a vector subtraction (Details here)
• The result of this subtraction is $\mathbf\small{\vec{r}_{1,2}}$
• It is the vector pointing from m1 to m2
4. We must clearly write about the convention to be followed while writing the distance vector between two masses. We can write it in 3 steps:
(i) There will be two numbers in the subscript
(ii) The first number indicates the mass from which the vector is drawn
♦ It is the tail end of the vector
(iii) The second number indicates the mass to which the vector is drawn
♦ It is the head end of the vector
5. The vector $\mathbf\small{\vec{r}_{1,2}}$ is our required mathematical fix
If we have $\mathbf\small{\vec{r}_{1,2}}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get the exact line through which the $\mathbf\small{\vec{F}_G}$ acts
6. The same $\mathbf\small{|\vec{F}_G|}$ acts on both m1 and m2
■ But force on m1 acts from m1 towards m2. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
■ And, force on m2 acts from m2 towards m1. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
7. We must clearly write the convention to be followed while writing the force vector between two masses. We can write it in 3 steps:
(i) There will be two numbers in the subscript
(ii) The first number indicates the 'mass which exerts the pull'
♦ The head end of the vector is directed towards this mass
(iii) The second number indicates the 'mass which is being pulled'
♦ The tail end of the vector is situated on this mass
8. Now we can write the forces using 'unit vectors'
■ Case 1: The force $\mathbf\small{\vec{F}_{G(2,1)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(2,1)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$
• So we get: $\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$
(iii) So our next aim is to find the unit vector $\mathbf\small{\hat{r}_{1,2}}$
• Clearly, if we divide $\mathbf\small{\vec{r}_{1,2}}$ by it's magnitude, we will get that required unit vector
• That is: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
(v) Note that, the direction of $\mathbf\small{\vec{F}_{G(2,1)}}$ is same as the direction of $\mathbf\small{\vec{r}_{1,2}}$
■ Case 2: The force $\mathbf\small{\vec{F}_{G(1,2)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(1,2)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$
• So we get: $\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$
• Note that a negative sign has to be introduced because, direction of $\mathbf\small{\vec{F}_{G(1,2)}}$ is opposite to the direction of $\mathbf\small{\hat{r}_{1,2}}$
(iii) We have already calculated the unit vector $\mathbf\small{\hat{r}_{1,2}}$ in case 1: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
9. Comparing the two cases, we see that:
Magnitudes are the same. The only difference is in direction
• So we can write: $\mathbf\small{\vec{F}_{G(1,2)}=-\vec{F}_{G(2,1)}}$
10. In general, we will be dealing with situations similar to case 2
This can be explained in 5 steps:
(i) Initially, we will be having an object of mass m1
(ii) We will be asked to find the gravitational force (exerted by m1) on a new object of mass m2
(iii) We will be measuring the distance from m1 to m2
• So the distance vector will be $\mathbf\small{\vec{r}_{1,2}}$. Not $\mathbf\small{\vec{r}_{2,1}}$
(iv) The required force will be $\mathbf\small{\vec{F}_{G(1,2)}}$
♦ It is the force exerted by m1 on m2
♦ It will be acting from m2 towards m1
(v) So $\mathbf\small{\vec{F}_{G(1,2)}}$ and $\mathbf\small{\vec{r}_{1,2}}$ will be in opposite directions
• Thus the (-)ve sign will be always present. We can write:
Eq.8.2: $\mathbf\small{\vec{F}_G=-\left[G\frac{m_1\; m_2}{|\vec{r}|^3}\right]\vec{r}}$
1. We have a force of attraction $\mathbf\small{|\vec{F}_G|}$ between two masses m1 and m2
• Consider the line joining the 'center of m1' and 'center of m2'
■ The $\mathbf\small{|\vec{F}_G|}$ will be acting along this line
• We need to fix up this line mathematically
• For that, we use vectors
2. Fig.8.10 below shows the two masses in 3D space
 |
| Fig.8.10 |
• If we have $\mathbf\small{\vec{r}_1}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m1 in 3D space (Details here)
(ii) $\mathbf\small{\vec{r}_2}$ is the position vector of m2
• If we have $\mathbf\small{\vec{r}_2}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m2 in 3D space
3. Subtract $\mathbf\small{\vec{r}_2}$ from $\mathbf\small{\vec{r}_1}$
• Remember that, it should be a vector subtraction (Details here)
• The result of this subtraction is $\mathbf\small{\vec{r}_{1,2}}$
• It is the vector pointing from m1 to m2
4. We must clearly write about the convention to be followed while writing the distance vector between two masses. We can write it in 3 steps:
(i) There will be two numbers in the subscript
(ii) The first number indicates the mass from which the vector is drawn
♦ It is the tail end of the vector
(iii) The second number indicates the mass to which the vector is drawn
♦ It is the head end of the vector
5. The vector $\mathbf\small{\vec{r}_{1,2}}$ is our required mathematical fix
If we have $\mathbf\small{\vec{r}_{1,2}}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get the exact line through which the $\mathbf\small{\vec{F}_G}$ acts
6. The same $\mathbf\small{|\vec{F}_G|}$ acts on both m1 and m2
■ But force on m1 acts from m1 towards m2. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
■ And, force on m2 acts from m2 towards m1. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
7. We must clearly write the convention to be followed while writing the force vector between two masses. We can write it in 3 steps:
(i) There will be two numbers in the subscript
(ii) The first number indicates the 'mass which exerts the pull'
♦ The head end of the vector is directed towards this mass
(iii) The second number indicates the 'mass which is being pulled'
♦ The tail end of the vector is situated on this mass
8. Now we can write the forces using 'unit vectors'
■ Case 1: The force $\mathbf\small{\vec{F}_{G(2,1)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(2,1)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$
• So we get: $\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$
(iii) So our next aim is to find the unit vector $\mathbf\small{\hat{r}_{1,2}}$
• Clearly, if we divide $\mathbf\small{\vec{r}_{1,2}}$ by it's magnitude, we will get that required unit vector
• That is: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
(v) Note that, the direction of $\mathbf\small{\vec{F}_{G(2,1)}}$ is same as the direction of $\mathbf\small{\vec{r}_{1,2}}$
■ Case 2: The force $\mathbf\small{\vec{F}_{G(1,2)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(1,2)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$
• So we get: $\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$
• Note that a negative sign has to be introduced because, direction of $\mathbf\small{\vec{F}_{G(1,2)}}$ is opposite to the direction of $\mathbf\small{\hat{r}_{1,2}}$
(iii) We have already calculated the unit vector $\mathbf\small{\hat{r}_{1,2}}$ in case 1: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
9. Comparing the two cases, we see that:
Magnitudes are the same. The only difference is in direction
• So we can write: $\mathbf\small{\vec{F}_{G(1,2)}=-\vec{F}_{G(2,1)}}$
10. In general, we will be dealing with situations similar to case 2
This can be explained in 5 steps:
(i) Initially, we will be having an object of mass m1
(ii) We will be asked to find the gravitational force (exerted by m1) on a new object of mass m2
(iii) We will be measuring the distance from m1 to m2
• So the distance vector will be $\mathbf\small{\vec{r}_{1,2}}$. Not $\mathbf\small{\vec{r}_{2,1}}$
(iv) The required force will be $\mathbf\small{\vec{F}_{G(1,2)}}$
♦ It is the force exerted by m1 on m2
♦ It will be acting from m2 towards m1
(v) So $\mathbf\small{\vec{F}_{G(1,2)}}$ and $\mathbf\small{\vec{r}_{1,2}}$ will be in opposite directions
• Thus the (-)ve sign will be always present. We can write:
Eq.8.2: $\mathbf\small{\vec{F}_G=-\left[G\frac{m_1\; m_2}{|\vec{r}|^3}\right]\vec{r}}$
• The above equation 8.2 is applicable to point masses only. In real world, we will be dealing with extended objects. We have already seen the difference between point masses and extended objects in the previous chapter (Details here)
• In the next section, we will see how to apply the equation to extended objects
• Before that, we will see some situations involving point masses only. We will write it in steps:
1. In the fig.8.11 below, we see four point masses m1, m2, m3 and m4
• They are distributed in a 3D space
• The distances between the 4 masses are denoted by $\mathbf\small{(\vec{r}_{2,1}),\;(\vec{r}_{3,1}),\;\rm{and} \;(\vec{r}_{4,1})}$
2. The 4 masses will be exerting forces on each other
■ We want to find the net force experienced by any single mass, say m1
3. The free body diagram of m1 is shown in fig.b
• In free body diagrams, we draw only those forces which are acting on the object under consideration. We do not draw those forces which are exerted by the object under consideration
• So we need to draw only those forces which the other masses exert on m1. We need not consider those forces which m1 exerts on others
4. We can write the force vectors directly
(i) Force exerted by m2 on m1: $\mathbf\small{\vec{F}_{G(2,1)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1}}$
• Based on the conventions that we wrote above, we have:
♦ $\mathbf\small{\vec{F}_{G(2,1)}}$ is the force exerted by m2 on m1
♦ It acts from m1 towards m2
♦ $\mathbf\small{\vec{r}_{2,1}}$ is the distance vector between m1 and m2
♦ It is drawn from m2 to m1
• So $\mathbf\small{\vec{F}_{G(2,1)}}$ and $\mathbf\small{\vec{r}_{2,1}}$ are in opposite directions. Thus the negative sign becomes necessary in (i)
• In a similar way, we can write the remaining 2 forces also
(ii) Force exerted by m3 on m1: $\mathbf\small{\vec{F}_{G(3,1)}=-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1}}$
(iii) Force exerted by m4 on m1: $\mathbf\small{\vec{F}_{G(4,1)}=-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1}}$
• The reader is advised to write 'why the -ve sign becomes necessary in (ii) and (iii)', in his/her own notebooks
Net force experienced $\mathbf\small{\vec{F}_{G}}$ by m1
= $\mathbf\small{\vec{F}_{G(2,1)}+\vec{F}_{G(3,1)}+\vec{F}_{G(4,1)}}$
= $\mathbf\small{\left(-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1} \right)+\left(-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1} \right)+\left(-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1} \right)}$
Solved example 8.7
In fig.8.12(a) below, three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC
(a) What is the force acting on a mass 2 m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled ?
Take AG = BG = CG = 1 m
Solution:
Part (a):
1. Any triangle will lie on a plane. So this is a 2D problem. We will need the x and y axes only. There is no need for the z-axis
• Assume that, the x-axis passes through the centroid G. Also assume that, the y-axis pass through the top vertex A
• So the two axes will intersect at G
• Thus G will be the origin of the axes. This is shown in fig.b
2. For any equilateral triangle:
(i) G will be equidistant from all the 3 vertices
(ii) Consider any vertex, say C
• The angle BCA at C will be 60o
• The line CG will bisect the 60o at that vertex
♦ So the angle BCG = 30o
• So GC will make an angle of 30o with the horizontal
♦ Consequently, GC will make 60o with the vertical
• In the same way, GB will also make 30o with the horizontal
♦ Consequently, GB will make 60o with the vertical
• GA is purely vertical
♦ It makes an angle of 90o with the horizontal
♦ It makes 0o with the vertical
(iii) AG is extended downwards to meet the base BC at D
• Since it is an equilateral triangle, D will be the midpoint of BC
• Also, AD will be perpendicular to BC
• Since D is the midpoint of BC, the line AD is a median
• The centroid G will divide the median AD in the ratio 2:1
(iv) Consider any vertex
• It's distance from G will be same as for the other two vertices
• So we have: AG = BG = CG
♦ In this problem, we are given that AG = BG = CG = 1 m
3. Now we can begin the calculations:
• The distance vectors are shown in fig.8.13(a) below:
• The free body diagram of the 2m mass at G is shown in fig.13(b)
4. Force due to mass at B
(i) $\mathbf\small{\vec{F}_{G(B,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[2Gm^2\right]\vec{r}_{B,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{B,G}}$ in component form
• To reach G from B:
♦ First we travel a distance BD horizontally to the right
♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{B,G}}$ are $\mathbf\small{(BD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{B,G}=(BD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(B,G)}=-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]}$
5. Force due to mass at C
(i) $\mathbf\small{\vec{F}_{G(C,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[2Gm^2\right]\vec{r}_{C,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{C,G}}$ in component form
• To reach G from C:
♦ First we travel a distance CD horizontally to the left
♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{C,G}}$ are $\mathbf\small{-(CD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{C,G}=-(CD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(CD)\hat{i}+(DG)\hat{j}]}$
(iv) But BD = CD
So the result in (iii) can be written as:
$\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]}$
6. Force due to mass at A
(i) $\mathbf\small{\vec{F}_{G(A,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{A,G}|^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[2Gm^2\right]\vec{r}_{A,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{A,G}}$ in component form
• To reach G from A:
♦ We have no horizontal distance to travel
♦ We travel only a distance AG vertically down
• So the components of $\mathbf\small{\vec{r}_{A,G}}$ are $\mathbf\small{(0)\hat{i}}$ and $\mathbf\small{-(AG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{A,G}=-(AG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(A,G)}=-\left[2Gm^2\right][-\hat{j}]}$
7. When we add the results in (4), (5) and (6), we get the net force experienced by the mass at G
So we can write:
The net force experienced by the mass at G
= $\mathbf\small{\vec{F}_{G(B,G)}+\vec{F}_{G(C,G)}+\vec{F}_{G(A,G)}}$
= $\mathbf\small{\left(-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$
• We see that, the two terms with BD will cancel each other. We get:
The net force experienced by the mass at G
= $\mathbf\small{\left([-2Gm^2(DG)\hat{j}]\right)+\left([-2Gm^2(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(AG)\hat{j}]\right)}$
8. The centroid G divides the median AD in the ratio 2:1
• That means AG = 2 times DG
• So the result in (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(4Gm^2[(DG)\hat{j}]\right)=0}$
■ Thus the net force on the mass at G is zero
• In (4) we wrote: $\mathbf\small{\vec{r}_{B,G}=(BD)\hat{i}+(DG)\hat{j}}$
• We can use trigonometry and thus avoid point D
(Then, we will be able to directly use the given distances: BG, CG and AG)
• We have: $\mathbf\small{\vec{r}_{B,G}=(BG\cos30)\hat{i}+(BG\sin30)\hat{j}}$
• Similarly, $\mathbf\small{\vec{r}_{C,G}}$ can also be written in terms of angles
• The reader is advised to write all steps using this alternate method and prove that, the net force on the object at G is zero
• In the next section, we will see how to apply the equation to extended objects
• Before that, we will see some situations involving point masses only. We will write it in steps:
1. In the fig.8.11 below, we see four point masses m1, m2, m3 and m4
• They are distributed in a 3D space
• The distances between the 4 masses are denoted by $\mathbf\small{(\vec{r}_{2,1}),\;(\vec{r}_{3,1}),\;\rm{and} \;(\vec{r}_{4,1})}$
 |
| Fig.8.11 |
■ We want to find the net force experienced by any single mass, say m1
3. The free body diagram of m1 is shown in fig.b
• In free body diagrams, we draw only those forces which are acting on the object under consideration. We do not draw those forces which are exerted by the object under consideration
• So we need to draw only those forces which the other masses exert on m1. We need not consider those forces which m1 exerts on others
4. We can write the force vectors directly
(i) Force exerted by m2 on m1: $\mathbf\small{\vec{F}_{G(2,1)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1}}$
• Based on the conventions that we wrote above, we have:
♦ $\mathbf\small{\vec{F}_{G(2,1)}}$ is the force exerted by m2 on m1
♦ It acts from m1 towards m2
♦ $\mathbf\small{\vec{r}_{2,1}}$ is the distance vector between m1 and m2
♦ It is drawn from m2 to m1
• So $\mathbf\small{\vec{F}_{G(2,1)}}$ and $\mathbf\small{\vec{r}_{2,1}}$ are in opposite directions. Thus the negative sign becomes necessary in (i)
• In a similar way, we can write the remaining 2 forces also
(ii) Force exerted by m3 on m1: $\mathbf\small{\vec{F}_{G(3,1)}=-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1}}$
(iii) Force exerted by m4 on m1: $\mathbf\small{\vec{F}_{G(4,1)}=-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1}}$
• The reader is advised to write 'why the -ve sign becomes necessary in (ii) and (iii)', in his/her own notebooks
5. The net force experienced by m1 will be the vector sum of the 3 forces written in (4)
So we can write:Net force experienced $\mathbf\small{\vec{F}_{G}}$ by m1
= $\mathbf\small{\vec{F}_{G(2,1)}+\vec{F}_{G(3,1)}+\vec{F}_{G(4,1)}}$
= $\mathbf\small{\left(-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1} \right)+\left(-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1} \right)+\left(-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1} \right)}$
Now we will see some solved examples
In fig.8.12(a) below, three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC
 |
| Fig.8.12 |
(b) What is the force if the mass at the vertex A is doubled ?
Take AG = BG = CG = 1 m
Solution:
Part (a):
1. Any triangle will lie on a plane. So this is a 2D problem. We will need the x and y axes only. There is no need for the z-axis
• Assume that, the x-axis passes through the centroid G. Also assume that, the y-axis pass through the top vertex A
• So the two axes will intersect at G
• Thus G will be the origin of the axes. This is shown in fig.b
2. For any equilateral triangle:
(i) G will be equidistant from all the 3 vertices
(ii) Consider any vertex, say C
• The angle BCA at C will be 60o
• The line CG will bisect the 60o at that vertex
♦ So the angle BCG = 30o
• So GC will make an angle of 30o with the horizontal
♦ Consequently, GC will make 60o with the vertical
• In the same way, GB will also make 30o with the horizontal
♦ Consequently, GB will make 60o with the vertical
• GA is purely vertical
♦ It makes an angle of 90o with the horizontal
♦ It makes 0o with the vertical
(iii) AG is extended downwards to meet the base BC at D
• Since it is an equilateral triangle, D will be the midpoint of BC
• Also, AD will be perpendicular to BC
• Since D is the midpoint of BC, the line AD is a median
• The centroid G will divide the median AD in the ratio 2:1
(iv) Consider any vertex
• It's distance from G will be same as for the other two vertices
• So we have: AG = BG = CG
♦ In this problem, we are given that AG = BG = CG = 1 m
3. Now we can begin the calculations:
• The distance vectors are shown in fig.8.13(a) below:
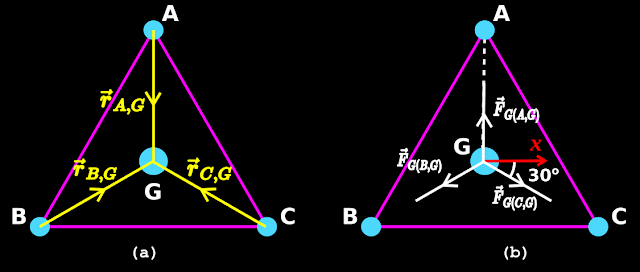 |
| Fig.8.13 |
4. Force due to mass at B
(i) $\mathbf\small{\vec{F}_{G(B,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[2Gm^2\right]\vec{r}_{B,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{B,G}}$ in component form
• To reach G from B:
♦ First we travel a distance BD horizontally to the right
♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{B,G}}$ are $\mathbf\small{(BD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{B,G}=(BD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(B,G)}=-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]}$
5. Force due to mass at C
(i) $\mathbf\small{\vec{F}_{G(C,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[2Gm^2\right]\vec{r}_{C,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{C,G}}$ in component form
• To reach G from C:
♦ First we travel a distance CD horizontally to the left
♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{C,G}}$ are $\mathbf\small{-(CD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{C,G}=-(CD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(CD)\hat{i}+(DG)\hat{j}]}$
(iv) But BD = CD
So the result in (iii) can be written as:
$\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]}$
6. Force due to mass at A
(i) $\mathbf\small{\vec{F}_{G(A,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{A,G}|^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[2Gm^2\right]\vec{r}_{A,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{A,G}}$ in component form
• To reach G from A:
♦ We have no horizontal distance to travel
♦ We travel only a distance AG vertically down
• So the components of $\mathbf\small{\vec{r}_{A,G}}$ are $\mathbf\small{(0)\hat{i}}$ and $\mathbf\small{-(AG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{A,G}=-(AG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(A,G)}=-\left[2Gm^2\right][-\hat{j}]}$
7. When we add the results in (4), (5) and (6), we get the net force experienced by the mass at G
So we can write:
The net force experienced by the mass at G
= $\mathbf\small{\vec{F}_{G(B,G)}+\vec{F}_{G(C,G)}+\vec{F}_{G(A,G)}}$
= $\mathbf\small{\left(-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$
• We see that, the two terms with BD will cancel each other. We get:
The net force experienced by the mass at G
= $\mathbf\small{\left([-2Gm^2(DG)\hat{j}]\right)+\left([-2Gm^2(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(AG)\hat{j}]\right)}$
8. The centroid G divides the median AD in the ratio 2:1
• That means AG = 2 times DG
• So the result in (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(4Gm^2[(DG)\hat{j}]\right)=0}$
■ Thus the net force on the mass at G is zero
Another method:
• We can use trigonometry and thus avoid point D
(Then, we will be able to directly use the given distances: BG, CG and AG)
• We have: $\mathbf\small{\vec{r}_{B,G}=(BG\cos30)\hat{i}+(BG\sin30)\hat{j}}$
• Similarly, $\mathbf\small{\vec{r}_{C,G}}$ can also be written in terms of angles
• The reader is advised to write all steps using this alternate method and prove that, the net force on the object at G is zero
Part (b):
1. In this case, the forces due to B and C are same as in part (a)
• Only change is in the force due to A
• We need to change only the last term in 'part (a)(7)'
2. The interaction is between 'a mass 2m' and 'another mass 2m'
• So we have (2m × 2m) = 4m2
3. Thus step (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left([8Gm^2(DG)\hat{j}]\right)}$
= $\mathbf\small{[4Gm^2(DG)\hat{j}]}$
4. But AG = 2 times DG
• DG = 0.5AG = (0.5 × 1 m) = 0.5 m
• So the result in (3) becomes:
• The net force experienced by the mass at G
= $\mathbf\small{[4Gm^2(0.5)\hat{j}]}$
= $\mathbf\small{[2Gm^2\hat{j}]}$
5. The magnitude of the net force is $\mathbf\small{2Gm^2}$
• It acts in the vertically upward direction
• But in part (b), there is no symmetry about the horizontal line passing through G
1. In this case, the forces due to B and C are same as in part (a)
• Only change is in the force due to A
• We need to change only the last term in 'part (a)(7)'
2. The interaction is between 'a mass 2m' and 'another mass 2m'
• So we have (2m × 2m) = 4m2
3. Thus step (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left([8Gm^2(DG)\hat{j}]\right)}$
= $\mathbf\small{[4Gm^2(DG)\hat{j}]}$
4. But AG = 2 times DG
• DG = 0.5AG = (0.5 × 1 m) = 0.5 m
• So the result in (3) becomes:
• The net force experienced by the mass at G
= $\mathbf\small{[4Gm^2(0.5)\hat{j}]}$
= $\mathbf\small{[2Gm^2\hat{j}]}$
5. The magnitude of the net force is $\mathbf\small{2Gm^2}$
• It acts in the vertically upward direction
• Note that, in part (a), the arrangement of masses is in a symmetrical manner. So the forces cancel out, giving zero net force
■ The reader is advised to try the alternate method for part (b) also
In the next section, we will see a few more solved examples
No comments:
Post a Comment