In this chapter, we will see various details about units and measurements.
To measure any quantity, we need a unit. Let us see the significance of ‘unit’ by considering an example. We will write it in steps:
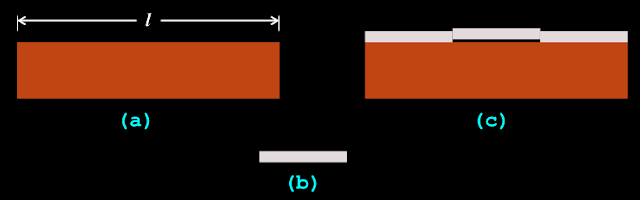
1. Fig.2.1(a) below shows a block of wood brought into a town for making furniture. The carpenter wants to know it’s length ‘l’.
2. Fig.b shows a steel rod that he usually uses to measure lengths. He calls that rod: cubit.
• That means, the length of that steel rod is considered as 1 cubit.
3. To find the length of the block, he places that steel rod end to end as shown in fig.c.
• We see that, the length of the block is 3 times the length of the steel rod.
• So the carpenter notes down in his book:
Length of the block = 3 cubits.
4. Here, 'cubit' is the unit used by the carpenters in that town to measure lengths.
• All carpenters in that town use the same rod (or it’s duplicates) to measure length.
5. Similarly, a vessel having appropriate volume ('appropriate' indicates not too small or too large based on the situation) can be selected to measure volume of oil, kerosene etc.,
• One such vessel was called 'amphora' in olden days.
• So 'amphora' is the unit for measuring volume in that town.
• All people in that town use that same vessel (or it’s duplicates) to measure volume.
Here also, we will see an example. We will write it in steps:
1. An engineer and his assistant is measuring the length of a wall.
• After taking the measurement, the engineer tells his assistant: 3.6
• The assistant notes it down.
2. After some time, another engineer and his assistant reaches there.
• They also measure the length.
• After taking the measurement, the engineer tells his assistant: 12
• The assistant notes it down.
3. The onlookers are puzzled. How can the same wall have two different lengths?
Another example:
1. Some oil is kept in a vessel in a town.
• An officer and his assistant reaches there and measure the volume of oil available.
• After taking the measurement, the officer tells his assistant: 800
• The assistant notes it down.
2. After some time, another officer and his assistant reaches there.
• They also measure the volume.
• After taking the measurement, the officer tells his assistant: 211
• The assistant notes it down.
3. The onlookers are puzzled. How can the same oil have two different volumes?
In the case of the wall:
1. The first engineer was using the unit ‘metre’.
• When he places '3 units plus 0.6 of his units' end to end, he will reach the other end of the wall.
2. The second engineer was using the unit ‘feet’.
• He has to place 12 of his units end to end to reach the other end of the wall.
■ Thus the two measurements gave different values.
In the case of oil:
1. The first officer was using the unit ‘litre’.
• When he uses his vessel 800 times, he will have measured out all the oil.
2. The second officer was using the unit ‘gallon’.
• When he uses his vessel 211 times, he will have measured out all the oil
■ Thus the two measurements gave different values.
Let us first see a brief history of units:
• In earlier times, scientists of different countries were using different systems of units.
• 3 such systems were prevalent until recently. They were:
1. The CGS system.
• In this system the base units were as follows:
♦ Base unit for Length was centimetre.
♦ Base unit for mass was gram.
♦ Base unit for time was second.
2. The FPS system.
In this system the base units were as follows:
♦ Base unit for Length was foot.
♦ Base unit for mass was pound.
♦ Base unit for time was second.
3. The MKS system.
In this system the base units were as follows:
♦ Base unit for Length was metre.
♦ Base unit for mass was kilogram.
♦ Base unit for time was second.
• In the year 1971, scientists from different parts of the world met at the General conference on weights and measures.
• At that conference, a new system was developed and recommended to be used internationally.
• This system was called Systeme Internationale d’ unites.
• ‘Systeme Internationale d’ unites’ is the French for 'International System of Units'.
• In every day usage, the scientific community refer to this system in an abbreviated form: SI system.
1. In the SI system, there are seven base quantities:
Length, mass, time, electric current, temperature, amount of substance and luminous intensity.
• The units of the seven base quantities are taken as the base units.
So the seven base units are:
1. Unit of length. It is called the metre. It's symbol is m.
2. Unit of mass. It is called the kilogram. It's symbol is kg.
3. Unit of Time. It is called the second. It's symbol is s.
4. Unit of electric current. It is called the ampere. It's symbol is A.
5. Unit of temperature. It is called the kelvin. It's symbol is K.
6. Unit of amount of substance. It is called the mole. It's symbol is mol.
7. Unit of luminous intensity. It is called the candela. It's symbol is cd.
Note: When mole is used, we have to specify the ‘type of entity' as well.
• Some examples:
♦ 2 moles of atoms.
♦ 5 moles of molecules.
♦ 3 mols of ions.
• Besides the seven base units that we saw above, there are two more:
(i) plane angle dθ (ii) solid angle d𝛀.
We will write about them in steps:
1. Consider fig.2.2(a) below:
• ds is the length of the arc AB.
• arc AB is a portion of a circle.
• O is the center of that circle.
• Arc AB subtends an angle dθ at O.
2. OA and OB are radii.
• Length of OA = Length of OB = r
• From our math classes, we know that $\mathbf\small{\text{angle}=\frac{\text{arc}}{\text{radius}}}$.
• So we get $\mathbf\small{d\theta=\frac{ds}{r}}$
■ Thus we get the definition for plane angle:
Plane angle dθ is the ratio of the arc length ds to the radius r
3. Consider fig.2.2(b).
• A 'portion of the surface of a sphere' is shown in red color. It has an area of dA.
• O is the center of that sphere. So the yellow lines are radii.
• The lengths of all the yellow lines are equal to r.
• The area dA subtends a solid angle d𝛀 at O.
4. The solid angle d𝛀 is given by $\mathbf\small{d\Omega=\frac{dA}{r^2}}$.
■ This gives the definition for solid angle.
Solid angle d𝛀 is the ratio of the area dA to the square of the radius r.
• For that, first, we have to see derived quantities.
• Let us see an example. We will write it in steps:
1. Consider the quantity: volume.
• Usually, we obtain volume by multiplying three items:
length, width and height.
2. width and height are also ‘lengths’.
• The quantity ‘volume’, is derived by multiplying the base quantity length, 3 times.
• So ‘volume’ is a derived quantity.
Another example:
1. Velocity is derived by dividing distance by time.
2. Both distance (length) and time are base quantities.
• So velocity is a derived quantity.
Now we can appreciate the difference between base units and derived units.
• We see that base quantities are independent quantities. Each of the seven base quantities can exist independently, with out any help from other quantities. Also none of the base quantities can be expressed in terms of other quantities. For example, mass cannot be expressed in terms of length or time or any other quantity.
• But derived quantities are dependent on base quantities. For example, we can write the volume of a wooden block only if we know the lengths (length, width and height) of that block.
Let us write the definitions:
■ The quantities which are not related to one another and cannot be expressed using other quantities are called base quantities. The units of base quantities are called base units.
■ Units which are expressed in terms of base units or those units which are dependent on base units are called derived units.
• There are only seven base units. But there are numerous derived units. We will see them in later chapters.
Let us see an example:
• In many situations, scientists have to measure 'energy'.
• At the general conference, the following decisions were made:
♦ The unit in which energy is to be measured is: joules.
♦ The symbol to be used for joules is J
Another example:
• In many situations, scientists have to measure 'electrical resistance'.
• At the general conference, the following decisions were made:
♦ The unit in which 'electrical resistance' is to be measured is: ohm
♦ The symbol to be used for ohm is 𝛀 (Greek capital letter Omega)
Let us see an example:
Volume of a container is 5 liters. Inside the container, some sand is present. Volume of that sand is 20 cm3. What percentage of the volume of the container is occupied by sand?
Solution:
1. To find percentage, both measurements must be in the same units.
• So we have to convert liters into cm3
2. One liter is the volume occupied by a cube of side 10 cm.
• That means 1 liter = 1000 cm3
• So 5 liters = 5000 cm3
• Thus we successfully converted the 'volume in liters' into 'volume in cm3'
3. Now we can find the percentage.
• The percentage volume occupied by sand = $\mathbf\small{\frac{20}{5000}\times 100}$ = 0.4 %
4. The conversion could be easily done in step (2) because, both liters and cubic centimeter are in the decimal system.
• If the conversion is not done, we would get: $\mathbf\small{\frac{20}{5}\times 100}$ = 400 %, which is absolutely wrong.
(1) The symbols of units are normally written using small letters in the English alphabet.
Some examples:
m (metre), s (second), kg (kilogram).
(2) But there are certain occasions in which capital letters of the English alphabet are used as symbols. The units named after persons are written like this.
Let us see some examples:
(i) The unit for measuring potential difference is volt.
• This unit is named after the scientist Alessandro Volta.
• So the symbol for the unit volt is V.
(ii) The unit for measuring pressure is pascal.
• This unit is named after the scientist Blaise Pascal.
• So the symbol for the unit pascal is P.
(iii) The unit for measuring force is newton.
• This unit is named after the scientist Sir Isaac Newton.
• So the symbol for the unit newton is N.
(3) While writing the 'names of units' never use capital letters.
Let us see some examples:
(i) kelvin is the SI unit for measuring temperature.
• When writing it as the name of the scientist Lord kelvin, write it as: Kelvin.
• When writing it as the unit, write it as: kelvin.
(ii) newton is the SI unit for measuring force.
• When writing it as the name of the scientist Sir Isaac Newton, write it as: Newton.
• When writing it as the unit, write it as: newton.
(4) Never use the plural form for symbols.
Some examples:
• 10 kg (correct) 10 kgs (wrong).
• 75 cm (correct) 75 cms (wrong).
(5) Never use full stop or comma after a symbol except at the end of a sentence.
An example:
• 75 cm is the length of a table. (correct).
• 75 cm. is the length of a table. (wrong).
(6) While writing derived units a slash (/) is used to denote division. But never use more than one slash in one derived unit.
An example:
• m/s2 (correct) m/s/s (wrong).
(7) When a derived unit is expressed as the product of other units use a dot or a space between them.
An example: N.m or N m
(8) Do not mix the name of a unit with the symbol.
Some examples:
• kg/m3 (correct).
• kilogram per cubic metre (correct).
• kg/cubic metre (wrong).
• kilogram per m3 (wrong).
• kg per m3 (wrong).
• kilogram/m3 (wrong).
• kilogram/cubic metre (wrong).
(9) While writing units along with a value, there must be single space between them.
Some examples:
• 273 K (correct) 273K (wrong).
• 100 m (correct) 100m (wrong).
(10) Never use more than one unit to express a physical quantity.
An example:
10.25 m ( correct) 10 m 25 cm (wrong).
■ The above given are basic rules. For a detailed information and for more such rules, the reader is advised to refer standard textbooks.
To measure any quantity, we need a unit. Let us see the significance of ‘unit’ by considering an example. We will write it in steps:
1. Fig.2.1(a) below shows a block of wood brought into a town for making furniture. The carpenter wants to know it’s length ‘l’.
 |
| Fig.2.1 |
• That means, the length of that steel rod is considered as 1 cubit.
3. To find the length of the block, he places that steel rod end to end as shown in fig.c.
• We see that, the length of the block is 3 times the length of the steel rod.
• So the carpenter notes down in his book:
Length of the block = 3 cubits.
4. Here, 'cubit' is the unit used by the carpenters in that town to measure lengths.
• All carpenters in that town use the same rod (or it’s duplicates) to measure length.
5. Similarly, a vessel having appropriate volume ('appropriate' indicates not too small or too large based on the situation) can be selected to measure volume of oil, kerosene etc.,
• One such vessel was called 'amphora' in olden days.
• So 'amphora' is the unit for measuring volume in that town.
• All people in that town use that same vessel (or it’s duplicates) to measure volume.
• So we see the importance of ‘units’. With out specifying a unit, we cannot measure quantities.
♦ That unit should be acceptable to all.
• Next we will see why it is important to standardize various units:
♦ That unit should be acceptable to all.
• Next we will see why it is important to standardize various units:
Here also, we will see an example. We will write it in steps:
1. An engineer and his assistant is measuring the length of a wall.
• After taking the measurement, the engineer tells his assistant: 3.6
• The assistant notes it down.
2. After some time, another engineer and his assistant reaches there.
• They also measure the length.
• After taking the measurement, the engineer tells his assistant: 12
• The assistant notes it down.
3. The onlookers are puzzled. How can the same wall have two different lengths?
Another example:
1. Some oil is kept in a vessel in a town.
• An officer and his assistant reaches there and measure the volume of oil available.
• After taking the measurement, the officer tells his assistant: 800
• The assistant notes it down.
2. After some time, another officer and his assistant reaches there.
• They also measure the volume.
• After taking the measurement, the officer tells his assistant: 211
• The assistant notes it down.
3. The onlookers are puzzled. How can the same oil have two different volumes?
Let us analyze each incidents described above:
1. The first engineer was using the unit ‘metre’.
• When he places '3 units plus 0.6 of his units' end to end, he will reach the other end of the wall.
2. The second engineer was using the unit ‘feet’.
• He has to place 12 of his units end to end to reach the other end of the wall.
■ Thus the two measurements gave different values.
In the case of oil:
1. The first officer was using the unit ‘litre’.
• When he uses his vessel 800 times, he will have measured out all the oil.
2. The second officer was using the unit ‘gallon’.
• When he uses his vessel 211 times, he will have measured out all the oil
■ Thus the two measurements gave different values.
This is a very serious issue. Suppose that, scientists and engineers from different parts of the world are collaborating on a project. Even if all of them speak English, none of them will be able to understand what the others are saying. The project will not materialize. The importance of using standardized units is obvious.
Let us first see a brief history of units:
• In earlier times, scientists of different countries were using different systems of units.
• 3 such systems were prevalent until recently. They were:
1. The CGS system.
• In this system the base units were as follows:
♦ Base unit for Length was centimetre.
♦ Base unit for mass was gram.
♦ Base unit for time was second.
2. The FPS system.
In this system the base units were as follows:
♦ Base unit for Length was foot.
♦ Base unit for mass was pound.
♦ Base unit for time was second.
3. The MKS system.
In this system the base units were as follows:
♦ Base unit for Length was metre.
♦ Base unit for mass was kilogram.
♦ Base unit for time was second.
• In the year 1971, scientists from different parts of the world met at the General conference on weights and measures.
• At that conference, a new system was developed and recommended to be used internationally.
• This system was called Systeme Internationale d’ unites.
• ‘Systeme Internationale d’ unites’ is the French for 'International System of Units'.
• In every day usage, the scientific community refer to this system in an abbreviated form: SI system.
Now we will see the details of the SI system. We will write them in steps:
Length, mass, time, electric current, temperature, amount of substance and luminous intensity.
• The units of the seven base quantities are taken as the base units.
So the seven base units are:
1. Unit of length. It is called the metre. It's symbol is m.
2. Unit of mass. It is called the kilogram. It's symbol is kg.
3. Unit of Time. It is called the second. It's symbol is s.
4. Unit of electric current. It is called the ampere. It's symbol is A.
5. Unit of temperature. It is called the kelvin. It's symbol is K.
6. Unit of amount of substance. It is called the mole. It's symbol is mol.
7. Unit of luminous intensity. It is called the candela. It's symbol is cd.
Note: When mole is used, we have to specify the ‘type of entity' as well.
• Some examples:
♦ 2 moles of atoms.
♦ 5 moles of molecules.
♦ 3 mols of ions.
• Besides the seven base units that we saw above, there are two more:
(i) plane angle dθ (ii) solid angle d𝛀.
We will write about them in steps:
1. Consider fig.2.2(a) below:
 |
| Fig.2.2 |
• arc AB is a portion of a circle.
• O is the center of that circle.
• Arc AB subtends an angle dθ at O.
2. OA and OB are radii.
• Length of OA = Length of OB = r
• From our math classes, we know that $\mathbf\small{\text{angle}=\frac{\text{arc}}{\text{radius}}}$.
• So we get $\mathbf\small{d\theta=\frac{ds}{r}}$
■ Thus we get the definition for plane angle:
Plane angle dθ is the ratio of the arc length ds to the radius r
3. Consider fig.2.2(b).
• A 'portion of the surface of a sphere' is shown in red color. It has an area of dA.
• O is the center of that sphere. So the yellow lines are radii.
• The lengths of all the yellow lines are equal to r.
• The area dA subtends a solid angle d𝛀 at O.
4. The solid angle d𝛀 is given by $\mathbf\small{d\Omega=\frac{dA}{r^2}}$.
■ This gives the definition for solid angle.
Solid angle d𝛀 is the ratio of the area dA to the square of the radius r.
• So now we have a basic idea about base units. Next we will see derived units.
• Let us see an example. We will write it in steps:
1. Consider the quantity: volume.
• Usually, we obtain volume by multiplying three items:
length, width and height.
2. width and height are also ‘lengths’.
• The quantity ‘volume’, is derived by multiplying the base quantity length, 3 times.
• So ‘volume’ is a derived quantity.
Another example:
1. Velocity is derived by dividing distance by time.
2. Both distance (length) and time are base quantities.
• So velocity is a derived quantity.
The units of derived quantities is called derived units.
An example:
• We get volume by multiplying length 3 times.
• So the unit of volume is obtained by multiplying the 'unit of length' 3 times.
• The SI unit of length is metre.
• Thus we get unit of volume as: m × m × m = m3
Another example:
• We get velocity by dividing distance by time.
• So the unit of velocity is obtained by dividing:
'unit of distance' by 'unit of time'.
• The SI unit of distance is metre.
• The SI unit of time is second.
• Thus we get unit of velocity as: m/s.
An example:
• We get volume by multiplying length 3 times.
• So the unit of volume is obtained by multiplying the 'unit of length' 3 times.
• The SI unit of length is metre.
• Thus we get unit of volume as: m × m × m = m3
Another example:
• We get velocity by dividing distance by time.
• So the unit of velocity is obtained by dividing:
'unit of distance' by 'unit of time'.
• The SI unit of distance is metre.
• The SI unit of time is second.
• Thus we get unit of velocity as: m/s.
Now we can appreciate the difference between base units and derived units.
• We see that base quantities are independent quantities. Each of the seven base quantities can exist independently, with out any help from other quantities. Also none of the base quantities can be expressed in terms of other quantities. For example, mass cannot be expressed in terms of length or time or any other quantity.
• But derived quantities are dependent on base quantities. For example, we can write the volume of a wooden block only if we know the lengths (length, width and height) of that block.
Let us write the definitions:
■ The quantities which are not related to one another and cannot be expressed using other quantities are called base quantities. The units of base quantities are called base units.
■ Units which are expressed in terms of base units or those units which are dependent on base units are called derived units.
• There are only seven base units. But there are numerous derived units. We will see them in later chapters.
At the international conference held in 1971, not only units, but also 'symbols' and ‘abbreviations’ were standardized.
• In many situations, scientists have to measure 'energy'.
• At the general conference, the following decisions were made:
♦ The unit in which energy is to be measured is: joules.
♦ The symbol to be used for joules is J
Another example:
• In many situations, scientists have to measure 'electrical resistance'.
• At the general conference, the following decisions were made:
♦ The unit in which 'electrical resistance' is to be measured is: ohm
♦ The symbol to be used for ohm is 𝛀 (Greek capital letter Omega)
Since the SI units use the decimal system, conversions within the system can be done easily.
Volume of a container is 5 liters. Inside the container, some sand is present. Volume of that sand is 20 cm3. What percentage of the volume of the container is occupied by sand?
Solution:
1. To find percentage, both measurements must be in the same units.
• So we have to convert liters into cm3
2. One liter is the volume occupied by a cube of side 10 cm.
• That means 1 liter = 1000 cm3
• So 5 liters = 5000 cm3
• Thus we successfully converted the 'volume in liters' into 'volume in cm3'
3. Now we can find the percentage.
• The percentage volume occupied by sand = $\mathbf\small{\frac{20}{5000}\times 100}$ = 0.4 %
4. The conversion could be easily done in step (2) because, both liters and cubic centimeter are in the decimal system.
• If the conversion is not done, we would get: $\mathbf\small{\frac{20}{5}\times 100}$ = 400 %, which is absolutely wrong.
Next we will see some basic rules to be followed while writing units.
(1) The symbols of units are normally written using small letters in the English alphabet.
Some examples:
m (metre), s (second), kg (kilogram).
(2) But there are certain occasions in which capital letters of the English alphabet are used as symbols. The units named after persons are written like this.
Let us see some examples:
(i) The unit for measuring potential difference is volt.
• This unit is named after the scientist Alessandro Volta.
• So the symbol for the unit volt is V.
(ii) The unit for measuring pressure is pascal.
• This unit is named after the scientist Blaise Pascal.
• So the symbol for the unit pascal is P.
(iii) The unit for measuring force is newton.
• This unit is named after the scientist Sir Isaac Newton.
• So the symbol for the unit newton is N.
(3) While writing the 'names of units' never use capital letters.
Let us see some examples:
(i) kelvin is the SI unit for measuring temperature.
• When writing it as the name of the scientist Lord kelvin, write it as: Kelvin.
• When writing it as the unit, write it as: kelvin.
(ii) newton is the SI unit for measuring force.
• When writing it as the name of the scientist Sir Isaac Newton, write it as: Newton.
• When writing it as the unit, write it as: newton.
(4) Never use the plural form for symbols.
Some examples:
• 10 kg (correct) 10 kgs (wrong).
• 75 cm (correct) 75 cms (wrong).
(5) Never use full stop or comma after a symbol except at the end of a sentence.
An example:
• 75 cm is the length of a table. (correct).
• 75 cm. is the length of a table. (wrong).
(6) While writing derived units a slash (/) is used to denote division. But never use more than one slash in one derived unit.
An example:
• m/s2 (correct) m/s/s (wrong).
(7) When a derived unit is expressed as the product of other units use a dot or a space between them.
An example: N.m or N m
(8) Do not mix the name of a unit with the symbol.
Some examples:
• kg/m3 (correct).
• kilogram per cubic metre (correct).
• kg/cubic metre (wrong).
• kilogram per m3 (wrong).
• kg per m3 (wrong).
• kilogram/m3 (wrong).
• kilogram/cubic metre (wrong).
(9) While writing units along with a value, there must be single space between them.
Some examples:
• 273 K (correct) 273K (wrong).
• 100 m (correct) 100m (wrong).
(10) Never use more than one unit to express a physical quantity.
An example:
10.25 m ( correct) 10 m 25 cm (wrong).
■ The above given are basic rules. For a detailed information and for more such rules, the reader is advised to refer standard textbooks.
In the next section, we will see details about Length.
No comments:
Post a Comment