In the previous section, we saw the work-energy theorem for a variable force.
• We saw that, even if the force acting on an object is not a steady constant force, the change in kinetic energy will be equal to the total work done by the force on the object.
• In this section, we will see some solved examples.
Solved example 6.9
A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m.
The frictional force is 50 N
(a) Plot the following two graphs:
(i) Force applied by the woman versus displacement
(ii) Frictional force versus displacement
(b) Calculate the work done by the two forces over 20 m
Solution:
Part (a):
1. Upto 10 m, the force is constant. So the graph will be a horizontal line for the first 10 m
2. The total distance is given as 20 m. So for the second 10 m, a variable force is applied
• Given that this force 'reduces linearly'. That means, the variation in the force is 'uniform'
• So the graph will be a sloping line
3. The frictional force is constant. But it is negative because it acts in a direction opposite to that of the applied force
4. The 3 forces are shown in fig.6.15 below:
• The magenta horizontal line represent the force in (1)
• The cyan sloping line represent the force in (2)
• The yellow horizontal line represent the force in (3)
Part (b):
The work done by a force (constant or varying) is given by the enclosed area
The enclosed areas for each force is marked separately in fig.5.16 below:
• The work done by the magenta force (constant force applied by the woman)
= Area of magenta rectangle = 100 × 10 = 1000 J
• The work done by the cyan force (varying force applied by the woman)
= Area of cyan trapezium = [(100+50)⁄2 × 10] = 75 × 10 =750 J
■ Total work done by the woman = 1000 + 750 = 1750 J
■ The work done by the yellow force (frictional force)
= Area of yellow rectangle = -50 × 20 = -1000 J
Solved example 6.10
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.17(a) below. Find the work done during the displacement of 16 m
Solution:
1. Work done = Area enclosed by the Force graph
• This area is shown in fig.b
2. So we can write:
• Total work done = Area of magenta rectangle + Area of yellow triangle
♦ Area of magenta rectangle = 5 × (9-4) = 5 × 5 = 25 J
♦ Area of yellow triangle = 1⁄2 × 5 × (16-9) = 1⁄2 × 5 × (7) = 17.5 J
• Thus we get: Total work = 25 + 17.5 = 42.5 J
Solved example 6.11
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.18(a) below.
Find the work done in the following two cases:
(a) Work done when the object is displaced from x = -3 m to x = 0
(b) Work done when the object is displaced from x = 0 to x = 2 m
Solution:
1. Work done = Area enclosed by the Force graph
• This area is shown in fig.b
2. So we can write:
• Total work done = Area of magenta triangle + Area of yellow triangle + Area of brown trapezium
3. To find those areas, we need their sides
• We can use analytic geometry:
• From the given data in fig.a, the coordinates of the ends of the force graph (cyan line) are:
P(-3,10) and Q(2,10)
• Slope 'm' of the cyan line PQ = $\mathbf\small{\frac{y_2-y_1}{x_2-x_1}=\frac{10-(-10)}{2-(-3)}=\frac{20}{5}=4}$
• Equation of line PQ is given by: $\mathbf\small{y-y_1=m(x-x_1)\Rightarrow y-(-10)=4(x-(-3))}$
$\mathbf\small{\Rightarrow y-(-10)=4(x-(-3))}$
$\mathbf\small{\Rightarrow y+10=4x+12}$
$\mathbf\small{\Rightarrow y=4x+2}$
• PQ intersects the x axis at R
♦ Coordinates of R can be obtained by putting y = 0 in the equation of PQ
♦ Thus we get: R(-0.5,0)
• PQ intersects the y axis at S
♦ Coordinates of S can be obtained by putting x = 0 in the equation of PQ
♦ Thus we get: S(0,2)
• So we have all the required points
4. For the magenta triangle:
• Base = (3-0.5) = 2.5
• Height = 10
• So area = 1⁄2 × 2.5 × 10 = 12.5 J
■ This is negative energy because the force corresponding to this area lies below the x axis and so is negative
5. For the yellow triangle:
• Base = 0.5
• Height = 2
• So area = 1⁄2 × 0.5 × 2 = 0.5 J
6. For the brown trapezium:
• Height on left side = 2
• Height on right side = 10
• Base = 2
• So area = [(2+10)⁄2 × 2] = 6 × 2 =12 J
• We saw that, even if the force acting on an object is not a steady constant force, the change in kinetic energy will be equal to the total work done by the force on the object.
• In this section, we will see some solved examples.
Solved example 6.9
A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m.
The frictional force is 50 N
(a) Plot the following two graphs:
(i) Force applied by the woman versus displacement
(ii) Frictional force versus displacement
(b) Calculate the work done by the two forces over 20 m
Solution:
Part (a):
1. Upto 10 m, the force is constant. So the graph will be a horizontal line for the first 10 m
2. The total distance is given as 20 m. So for the second 10 m, a variable force is applied
• Given that this force 'reduces linearly'. That means, the variation in the force is 'uniform'
• So the graph will be a sloping line
3. The frictional force is constant. But it is negative because it acts in a direction opposite to that of the applied force
4. The 3 forces are shown in fig.6.15 below:
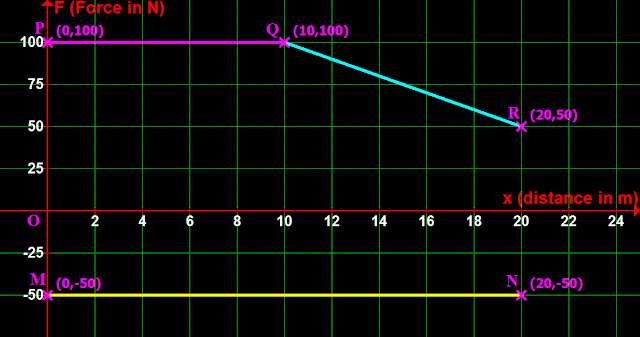 |
| Fig.6.15 |
• The cyan sloping line represent the force in (2)
• The yellow horizontal line represent the force in (3)
Part (b):
The work done by a force (constant or varying) is given by the enclosed area
The enclosed areas for each force is marked separately in fig.5.16 below:
 |
| Fig.6.16 |
= Area of magenta rectangle = 100 × 10 = 1000 J
• The work done by the cyan force (varying force applied by the woman)
= Area of cyan trapezium = [(100+50)⁄2 × 10] = 75 × 10 =750 J
■ Total work done by the woman = 1000 + 750 = 1750 J
■ The work done by the yellow force (frictional force)
= Area of yellow rectangle = -50 × 20 = -1000 J
Solved example 6.10
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.17(a) below. Find the work done during the displacement of 16 m
 |
| Fig.6.17 |
1. Work done = Area enclosed by the Force graph
• This area is shown in fig.b
2. So we can write:
• Total work done = Area of magenta rectangle + Area of yellow triangle
♦ Area of magenta rectangle = 5 × (9-4) = 5 × 5 = 25 J
♦ Area of yellow triangle = 1⁄2 × 5 × (16-9) = 1⁄2 × 5 × (7) = 17.5 J
• Thus we get: Total work = 25 + 17.5 = 42.5 J
Solved example 6.11
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.18(a) below.
 |
| Fig.6.18 |
(a) Work done when the object is displaced from x = -3 m to x = 0
(b) Work done when the object is displaced from x = 0 to x = 2 m
Solution:
1. Work done = Area enclosed by the Force graph
• This area is shown in fig.b
2. So we can write:
• Total work done = Area of magenta triangle + Area of yellow triangle + Area of brown trapezium
3. To find those areas, we need their sides
• We can use analytic geometry:
• From the given data in fig.a, the coordinates of the ends of the force graph (cyan line) are:
P(-3,10) and Q(2,10)
• Slope 'm' of the cyan line PQ = $\mathbf\small{\frac{y_2-y_1}{x_2-x_1}=\frac{10-(-10)}{2-(-3)}=\frac{20}{5}=4}$
• Equation of line PQ is given by: $\mathbf\small{y-y_1=m(x-x_1)\Rightarrow y-(-10)=4(x-(-3))}$
$\mathbf\small{\Rightarrow y-(-10)=4(x-(-3))}$
$\mathbf\small{\Rightarrow y+10=4x+12}$
$\mathbf\small{\Rightarrow y=4x+2}$
• PQ intersects the x axis at R
♦ Coordinates of R can be obtained by putting y = 0 in the equation of PQ
♦ Thus we get: R(-0.5,0)
• PQ intersects the y axis at S
♦ Coordinates of S can be obtained by putting x = 0 in the equation of PQ
♦ Thus we get: S(0,2)
• So we have all the required points
4. For the magenta triangle:
• Base = (3-0.5) = 2.5
• Height = 10
• So area = 1⁄2 × 2.5 × 10 = 12.5 J
■ This is negative energy because the force corresponding to this area lies below the x axis and so is negative
5. For the yellow triangle:
• Base = 0.5
• Height = 2
• So area = 1⁄2 × 0.5 × 2 = 0.5 J
6. For the brown trapezium:
• Height on left side = 2
• Height on right side = 10
• Base = 2
• So area = [(2+10)⁄2 × 2] = 6 × 2 =12 J
Now we can calculate the total works
Part (a): Work done when the object is displaced from x = -3 m to x = 0
• This is given by:
Area of magenta triangle + Area of yellow triangle
= -12.5+0.5 = -12 J
Part (b): Work done when the object is displaced from x = 0 m to x = 2 m
• This is given by:
Area of brown trapezium = 12 J
Solved example 6.12
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.17(a) below. Find the work done during the displacement from x = 1 to x = 5 m
Solution:
1. The area enclosed by the given graph (upto x = 5 m) can be considered to be made up of rectangles
2. The various areas are:
Area 1: 20 × 1 = 20 J (+ve)
Area 2: 40 × 1 = 40 J (+ve)
Area 3: 40 × 1 = 40 J (-ve)
Area 4: 20 × 1 = 20 J (+ve)
3. So work done = 20+40-40+20 = 40 J
Solved example 6.13
A 15 kg block is placed on a rough horizontal surface and is pulled by a horizontal force of 90 N. Coefficient of friction between the block and the floor is 0.4. Find the work done by each individual force acting on the block over a displacement of 8 m [Take g = 10 ms-2]
Solution:
• The FBD of the block will show all the forces acting on it. This is shown in fig.6.20(a) below:
• There are four forces. We will consider each separately
• Note that, $\mathbf\small{\vec{W}}$ and $\mathbf\small{\vec{F_N}}$ will cancel each other.
♦ That means, each of them becomes zero. Work done by a zero force is zero.
♦ However, we will apply the usual procedure (for finding work done) to them also
1. Force $\mathbf\small{\vec{W}}$
• This is the weight of the block. It acts vertically downwards
• But there is no displacement in the vertical direction. So work done by this force is zero
2. Force $\mathbf\small{\vec{F_N}}$
• This is the normal reaction from the floor. It acts vertically upwards
• But there is no displacement in the vertical direction. So work done by this force is zero
3. Force 90 N
• This force acts towards the right. This force is pulling the block
• The displacement is in the same direction as the force
• So work done = Force × displacement = 90 × 8 = 720 J
4. The frictional force $\mathbf\small{\vec{f_k}}$
• The magnitude of this force is given by μFN
• So magnitude = 0.4 × 15 × 10 = 60 N
• This force acts in a direction opposite to the displacement
• So we take frictional force as -60 N
• Then work done = Force × displacement = -60 × 8 = -480 J
■ Kinetic energy attained by the block during the displacement of 8 m
= Net work done = 720-480 = 240 J
Solved example 6.14
A body of mass 2 kg, initially at rest, moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction 0.1 Compute the
(a) Work done by applied force in 10 s
(b) Work done by friction in 10 s
(c) Work done by the net force on the body in 10 s
(d) Change in kinetic energy of the body in 10 s
[Take g = 9.8 ms-2]
Solution:
The FBD is shown in fig.6.20(b) above
1. First we want the displacement 'x' that takes place during the 10 s
• The initial velocity v0 is 0 ms-1
• The final velocity v has to be calculated
2. We can use the equation: $\mathbf\small{v=v_0 +at}$
3. a = Net force⁄mass = Applied force - frictional force⁄mass
Frictional force = μFN = 0.1 × 2 × 9.8 = 1.96 N
So a = 7 - 1.96⁄2 = 5.04⁄2 = 2.52 ms-2
4. Entering known values in (2), we get:
v = 0 + 2.52 × 10 = 25.2 ms-1
5. Now we can use the equation: $\mathbf\small{v^2-v_0^2=2ax}$
• Entering known values, we get: $\mathbf\small{25.2^2-0^2=2 \times 2.52 \times x}$
• From this we get: x = 126 m
6. So work done by the applied force = Force × displacement = 7 × 126 = 882 J
• This is the answer for part (a)
7. Work done by friction = Frictional force × displacement = 1.96 × 126 = 246.96 J
• This is the answer for part (b)
8. Net force = Applied force - frictional force = 7 - 1.96 = 5.04
• Work done by net force = Net force × displacement = 5.04 × 126 = 635.04 J
• This is the answer for part (c)
9. According to work-energy theorem, we have:
• Change in kinetic energy = Kf - Ki = work done by net force
• So change in kinetic energy = work done by net force = 635.04 J (from part (c))
• This is the answer for part (d)
Part (a): Work done when the object is displaced from x = -3 m to x = 0
• This is given by:
Area of magenta triangle + Area of yellow triangle
= -12.5+0.5 = -12 J
Part (b): Work done when the object is displaced from x = 0 m to x = 2 m
• This is given by:
Area of brown trapezium = 12 J
Solved example 6.12
The force F acting on an object moving in a straight line varies with distance as shown in the graph in fig.6.17(a) below. Find the work done during the displacement from x = 1 to x = 5 m
 |
| Fig.6.19 |
1. The area enclosed by the given graph (upto x = 5 m) can be considered to be made up of rectangles
2. The various areas are:
Area 1: 20 × 1 = 20 J (+ve)
Area 2: 40 × 1 = 40 J (+ve)
Area 3: 40 × 1 = 40 J (-ve)
Area 4: 20 × 1 = 20 J (+ve)
3. So work done = 20+40-40+20 = 40 J
Solved example 6.13
A 15 kg block is placed on a rough horizontal surface and is pulled by a horizontal force of 90 N. Coefficient of friction between the block and the floor is 0.4. Find the work done by each individual force acting on the block over a displacement of 8 m [Take g = 10 ms-2]
Solution:
• The FBD of the block will show all the forces acting on it. This is shown in fig.6.20(a) below:
 |
| Fig.6.20 |
• Note that, $\mathbf\small{\vec{W}}$ and $\mathbf\small{\vec{F_N}}$ will cancel each other.
♦ That means, each of them becomes zero. Work done by a zero force is zero.
♦ However, we will apply the usual procedure (for finding work done) to them also
1. Force $\mathbf\small{\vec{W}}$
• This is the weight of the block. It acts vertically downwards
• But there is no displacement in the vertical direction. So work done by this force is zero
2. Force $\mathbf\small{\vec{F_N}}$
• This is the normal reaction from the floor. It acts vertically upwards
• But there is no displacement in the vertical direction. So work done by this force is zero
3. Force 90 N
• This force acts towards the right. This force is pulling the block
• The displacement is in the same direction as the force
• So work done = Force × displacement = 90 × 8 = 720 J
4. The frictional force $\mathbf\small{\vec{f_k}}$
• The magnitude of this force is given by μFN
• So magnitude = 0.4 × 15 × 10 = 60 N
• This force acts in a direction opposite to the displacement
• So we take frictional force as -60 N
• Then work done = Force × displacement = -60 × 8 = -480 J
■ Kinetic energy attained by the block during the displacement of 8 m
= Net work done = 720-480 = 240 J
Solved example 6.14
A body of mass 2 kg, initially at rest, moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction 0.1 Compute the
(a) Work done by applied force in 10 s
(b) Work done by friction in 10 s
(c) Work done by the net force on the body in 10 s
(d) Change in kinetic energy of the body in 10 s
[Take g = 9.8 ms-2]
Solution:
The FBD is shown in fig.6.20(b) above
1. First we want the displacement 'x' that takes place during the 10 s
• The initial velocity v0 is 0 ms-1
• The final velocity v has to be calculated
2. We can use the equation: $\mathbf\small{v=v_0 +at}$
3. a = Net force⁄mass = Applied force - frictional force⁄mass
Frictional force = μFN = 0.1 × 2 × 9.8 = 1.96 N
So a = 7 - 1.96⁄2 = 5.04⁄2 = 2.52 ms-2
4. Entering known values in (2), we get:
v = 0 + 2.52 × 10 = 25.2 ms-1
5. Now we can use the equation: $\mathbf\small{v^2-v_0^2=2ax}$
• Entering known values, we get: $\mathbf\small{25.2^2-0^2=2 \times 2.52 \times x}$
• From this we get: x = 126 m
6. So work done by the applied force = Force × displacement = 7 × 126 = 882 J
• This is the answer for part (a)
7. Work done by friction = Frictional force × displacement = 1.96 × 126 = 246.96 J
• This is the answer for part (b)
8. Net force = Applied force - frictional force = 7 - 1.96 = 5.04
• Work done by net force = Net force × displacement = 5.04 × 126 = 635.04 J
• This is the answer for part (c)
9. According to work-energy theorem, we have:
• Change in kinetic energy = Kf - Ki = work done by net force
• So change in kinetic energy = work done by net force = 635.04 J (from part (c))
• This is the answer for part (d)
No comments:
Post a Comment