Chapter 8.5 - Gravitational Force Exerted by a Spherical Shell

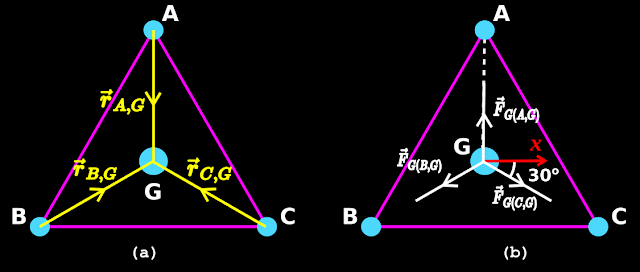
In the previous section, we completed a discussion on the magnitude as well as direction of the gravitational force of attraction. We also saw some solved examples. In all those examples, we were dealing with point masses. In this section we will see how the force acts between extended objects. We already saw the difference between point masses and extended objects here 

1. Consider an extended object like a block of wood. We will call it: A
2. A point mass is kept in the vicinity of A. We will call the point mass: B
3. So A is an extended object and B is a point mass
• We want to find the 'gravitational force of attraction' $\mathbf\small{\vec{F}_{G(A,B)}}$ exerted by A on B
4. In this case, each point mass in A will be exerting an attractive force on B
• So we will see a large number of force vectors
    ♦ All of them will be starting from B
    ♦ All of them will be pointing towards A
        ☆ But all of them will not be pointing towards a single point in A
        ☆ Different vectors will be pointing towards different points in A
5. So we can write:
■ The tail ends of all the force vectors will be the same point. But the head ends will be different
• That means, all the force vectors will be having different directions
6. Now, to obtain the resultant force on B, we must add all the force vectors
• It must be a vector addition
• Such a vector addition of different vectors can be done easily using the principles of calculus. We will see it in higher classes
7. However, for some 'simple extended objects', we can obtain the resultant, without the application of calculus

---

We will now see the case of a spherical shell, which is a 'simple extended object'. We will write it in steps 

1. Fig.8.18(a) below shows a spherical shell. We will call it: A 
• Note that, it is spherical in shape. And it is hollow inside. So in a 2D drawing, it will appear as a circle

Fig.8.18

2. A point mass is kept in the vicinity of A. We will call the point mass: B
3. So A is an extended object and B is a point mass
• We want to find the 'gravitational force of attraction' $\mathbf\small{\vec{F}_{G(A,B)}}$ exerted by A on B
4. The point mass B appears to be placed 'eccentrically' when compared to A. But that should not be a problem. We must be able to find the force $\mathbf\small{\vec{F}_{G(A,B)}}$ regardless of the position of B
5. In fig.b, the center of A is marked as O
• A white dashed line joins O and B
6. In fig.c, a 'random point mass' P is marked on A
• The force $\mathbf\small{\vec{F}_{G(P,B)}}$ is also shown
• We know that, this force will be directed from B towards P. This is indicated by the white dotted line
7. This force $\mathbf\small{\vec{F}_{G(P,B)}}$ can be resolved into two perpendicular components. This is shown in fig.8.19(a) below

Fig.8.19

• One component acts along OA. It is shown in red color
• The other component acts perpendicular to OA. It is shown in yellow color
8. Once a vector is resolved into it's two perpendicular components, we need to consider those two components only
• The 'combined effect produced by the two components' is same as the 'effect produced by $\mathbf\small{\vec{F}_{G(P,B)}}$'
• That means, we can ignore $\mathbf\small{\vec{F}_{G(P,B)}}$ and do calculations with the two components alone
9. In fig.8.19(b), another point mass P' is marked
• This P' has some peculiarities:
    ♦ P' and P are symmetric points. The axis of symmetry is OB
    ♦ P' is the one and only symmetric point of P (when the axis OB is considered)
10. Now we repeat all the works on P':
It can be summarized in 3 steps:
(i) $\mathbf\small{\vec{F}_{G(P',B)}}$ is the force exerted by P' on B
(ii) The red vector in fig.8.19(b) is the parallel component of $\mathbf\small{\vec{F}_{G(P',B)}}$
(iii) The yellow vector in fig.8.19(b) is the perpendicular component of $\mathbf\small{\vec{F}_{G(P',B)}}$
11. Now compare figs (a) and (b):
• Distances PB and P'B are equal. So the following two magnitudes are equal:
(i) Magnitude of $\mathbf\small{\vec{F}_{G(P,B)}}$
(ii) Magnitude of $\mathbf\small{\vec{F}_{G(P',B)}}$
• PB and P'B make the same angle with OB. So the following two magnitudes are also equal:
(i) Magnitude of the red vector in fig.a
(ii) Magnitude of the red vector in fig.b
• The following two magnitudes are also equal:
(i) Magnitude of the yellow vector in fig.a
(ii) Magnitude of the yellow vector in fig.b
12. We see something of interest:
• The red vectors in figs. (a) and (b) act in the same direction
    ♦ That means, parallel components add up
• The yellow vectors in figs. (a) and (b) act in the opposite directions
    ♦ That means, perpendicular components cancel each other
    ♦ Remember that, the magnitudes of the two yellow vectors are equal
13. Now, like P, we can consider any other point
• It will have a unique symmetric point on the other side of OB
• For those two points also, the parallel components will add up and the perpendicular components will cancel each other
• So in effect, there will be no force perpendicular to OB
■ All forces will be acting along OB
14. OB is the line joining the center of A to B
■ So we can write:
The point mass B will experience an attractive force towards the spherical shell A. This force will be appear as if all the mass of A is concentrated at it's centre O
15. The result written in (14) can be used in general:
■ If we want to find the 'force exerted by a spherical shell' on a 'point mass situated outside the shell', assume that, all the mass of the shell is concentrated at it's center, and then do the calculations

---

In the above discussion, the point mass B was outside the shell. Now we will consider the case when B is inside the shell. We will write it in steps 

1. Fig.8.20(a) below shows a spherical shell. We will call it: A 
• Note that, it is spherical in shape. And it is hollow inside. So in a 2D drawing, it will appear as a circle

Fig.8.20

2. A point mass is kept inside A. We will call the point mass: B
3. So A is an extended object and B is a point mass
• We want to find the 'gravitational force of attraction' $\mathbf\small{\vec{F}_{G(A,B)}}$ exerted by A on B
4. The point mass B appears to be placed 'eccentrically' inside A. But that should not be a problem. We must be able to find the force $\mathbf\small{\vec{F}_{G(A,B)}}$ regardless of the position of B
5. In fig.b, the center of A is marked as O
• A white dashed line joins O and B
6. In fig.b, a 'random point mass' is marked on A. It is shown in green color
• The force of attraction between the green point and B is also shown
    ♦ This force is indicated by the green vector
7. Now consider fig.8.21(a) below:

Fig.8.21

• The red dashed line is a chord of the circle
• This chord is drawn perpendicular to OB
8. The red dashed chord separates the circle into two parts
• The upper part is smaller
• The lower part is larger
9. A 'random point mass' is marked on the upper part. It is shown in yellow color
• The force of attraction between the yellow point and B is also shown
    ♦ This force is indicated by the yellow vector
10. Let us compare the magnitudes of the green and yellow vectors:
• Both act between 'a point mass on A' and B
• But for the yellow vector, the point mass is closer to B
• So the yellow vector will have a greater magnitude than the green vector
11. Now let us compare the directions of the green and yellow vectors:
• The green vector tries to pull B towards the lower portion of the shell
• The yellow vector tries to pull B towards the upper portion of the shell
12. So the green and yellow vectors are acting in somewhat opposite directions 
• Also we know that, the yellow vector has a greater magnitude
• So we would expect the point mass B to move towards the upper portion of the shell
13. But when we take a closer look, we find some thing of interest:
    ♦ We can mark numerous green points. Because the lower arc is larger
    ♦ But we cannot mark that many yellow points. Because the upper arc is smaller
• This is shown in fig.b 
■ That means:
    ♦ There will be numerous green vectors
    ♦ There will not be that many yellow vectors
14. We can write:
    ♦ The green vectors, though smaller in strengths, are greater in numbers
    ♦ The yellow vectors, though greater in strengths, are smaller in numbers
15. That means:
    ♦ The net upward force will be equal to the net downward force
    ♦ The two net forces will cancel each other
• We will see the precise mathematical proof in higher classes
• At present, all we need to know is this:
The net force on B is zero
16. The result written in (15) can be used in general:
■ The 'force exerted by a spherical shell' on a 'point mass situated inside the shell', is zero

---

• So we have seen the effects of a 'simple extended object'
• We chose a spherical shell to be the 'simple extended object'
• In later sections, we will see the applications of the results that we derived in this discussion
• In the next section, we will see an experiment which helps to obtain the value of the Universal gravitational constant G

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved

Chapter 8.4 - Solved Examples on Gravitational Force

In the previous section, we saw the magnitude of direction of the gravitational force of attraction . We also saw a solved example. In this section we will see a few more solved examples

Solved example 8.8
Find the unit of the universal gravitational constant G
Solution:
• We have: $\mathbf\small{|\vec{F}_{G}|=G\frac{m_1\; m_2}{|\vec{r}|^2}}$
• So we get: $\mathbf\small{G=\frac{|\vec{r}|^2\;|\vec{F}_{G}|}{m_1\; m_2}}$
• Thus the unit is: $\mathbf\small{N\,m^2\,kg^{-2}}$

Solved example 8.9
Two heavy bodies of masses 40 kg and 60 kg attract each other with a force of 4 × 10^-5 N. If G is 6 × 10^-11 N m² kg^-2, find the distance between them
Solution:
• We have: $\mathbf\small{|\vec{F}_{G}|=G\frac{m_1\; m_2}{|\vec{r}|^2}}$
• Substituting the given values, we get: $\mathbf\small{4\times 10^{-5}(N)=6\times 10^{-11}(N\,m^2\,kg^{-2})\left(\frac{40 (kg)\times 60(kg)}{|\vec{r}|^2} \right)}$
$\mathbf\small{\Rightarrow 4\times 10^{-5}=\left(\frac{1.44 \times 10^{-7}(m^2)}{|\vec{r}|^2} \right)}$
$\mathbf\small{\Rightarrow |\vec{r}|^2=\left(\frac{1.44 \times 10^{-7}(m^2)}{4\times 10^{-5}} \right)=0.0036\,(m^2)}$
$\mathbf\small{\Rightarrow |\vec{r}|=0.06\,m}$

Solved example 8.10
Two bodies A and B of masses M and 4M respectively, are placed at a distance of 2.73 m apart. Another body C of mass m is to be placed in between A and B in such a way that, the net force on C is zero. What is the distance of C from A
Solution:
1. Fig.8.14 (a) below shows the 3 bodies in a line
Let C be at a distance of  x m from A

Fig.8.14

2. Fig.b shows the free body diagram of C
(i) We have: $\mathbf\small{\vec{F}_{G(A,C)}=-\left[G\frac{M\times m}{|\vec{r}_{A,C}|^3}\right]\vec{r}_{A,C}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=-\left[G\frac{M\times m}{x^3}\right](x)(-\hat{i})}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=\left[\frac{GMm}{x^2}\right]\hat{i}}$

(ii) We have: $\mathbf\small{\vec{F}_{G(B,C)}=-\left[G\frac{m\times 4M}{|\vec{r}_{B,C}|^3}\right]\vec{r}_{B,C}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=-\left[G\frac{m\times 4M}{(2.73-x)^3}\right](2.73-x)\hat{i}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=-\left[\frac{4Gm M}{(2.73-x)^2}\right]\hat{i}}$
3. Net force = $\mathbf\small{\vec{F}_{G(A,C)}+\vec{F}_{G(B,C)}}$
⇒ Net force = $\mathbf\small{\left[\frac{GMm}{x^2}\right]\hat{i}+\left(-\left[\frac{4Gm M}{(2.73-x)^2}\right]\hat{i} \right)}$
4. But net force must be zero. So we get:
$\mathbf\small{\left[\frac{GMm}{x^2}\right]\hat{i}=\left[\frac{4Gm M}{(2.73-x)^2}\right]\hat{i}}$
• We have an equality of two vectors. So their magnitudes must be the same. We can write:
$\mathbf\small{\left[\frac{GMm}{x^2}\right]=\left[\frac{4Gm M}{(2.73-x)^2}\right]}$
$\mathbf\small{\Rightarrow \left[\frac{1}{x^2}\right]=\left[\frac{4}{(2.73-x)^2}\right]}$
$\mathbf\small{\Rightarrow (2.73-x)^2=4x^2}$ 
⇒ (2.73-x) = 2x (Taking roots on both sides)
⇒ 2.73 = 3x
⇒ x = 0.91 m

Solved example 8.11
Two bodies A and B have equal masses. The gravitational force of attraction between them is $\mathbf\small{\vec{F}_{G}}$. 25% of the mass of A is transferred to B. What is the new force of attraction
Solution:
1. Let the initial masses of the two bodies be m each 
• Then we can write: $\mathbf\small{\vec{F}_{G}=-\left[\frac{Gm^2}{|\vec{r}|^3}\right]\vec{r}}$
• Where $\mathbf\small{\vec{r}}$ is the distance vector between A and B
2. Final mass of A = (m-0.25m) = 0.75m
• Final mass of B = (m+0.25m) = 1.25m
3. New force $\mathbf\small{\vec{F}_{G(new)}=-\left[\frac{G(0.75m)(1.25m)}{|\vec{r}|^3}\right]\vec{r}=-\left[\frac{0.9375Gm^2}{|\vec{r}|^3}\right]\vec{r}}$
4. Dividing (3) by (1), we get:
$\mathbf\small{\frac{\vec{F}_{G(new)}}{\vec{F}_{G}}=\left(-\left[\frac{0.9375Gm^2}{|\vec{r}|^3}\right]\vec{r} \right)\div \left(-\left[\frac{Gm^2}{|\vec{r}|^3}\right]\vec{r} \right)=0.9375}$
$\mathbf\small{\Rightarrow \vec{F}_{G(new)}=0.9375\;\vec{F}_{G}}$

Solved example 8.12
Two bodies A and B have masses m and M respectively. The gravitational force of attraction between them is $\mathbf\small{\vec{F}}$. A third body C is placed in contact with A. The body C has a mass of 2m. What is the force on B due to A? What is the total force on B ?
Solution:
Part (a):
• Initially, there are only two masses A and B
• At that time, the force is given to be $\mathbf\small{\vec{F}}$
• We can write:
$\mathbf\small{\vec{F}=\vec{F}_{G(A,B)}=-\left[\frac{GmM}{|\vec{r}|^3}\right]\vec{r}}$
• Where $\mathbf\small{\vec{r}}$ is the distance vector between A and B
Part (b):
• When C is placed near A, the force on B due to C is given by:
$\mathbf\small{\vec{F}_{G(C,B)}=-\left[\frac{G\times 2m\times M}{|\vec{r}|^3}\right]\vec{r}}$
• Taking ratios, we get:
$\mathbf\small{\frac{\vec{F}_{G(C,B)}}{\vec{F}_{G(A,B)}}=\frac{\vec{F}_{G(C,B)}}{\vec{F}}=\left(-\left[\frac{G\times 2m\times M}{|\vec{r}|^3}\right]\vec{r} \right)\div \left(-\left[\frac{G\times m\times M}{|\vec{r}|^3}\right]\vec{r} \right)}$
$\mathbf\small{\Rightarrow \frac{\vec{F}_{G(C,B)}}{\vec{F}}=2}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,B)}=2\vec{F}}$
• Thus we can write:
Total force on B = $\mathbf\small{\vec{F}_{G(A,B)}+\vec{F}_{G(C,B)}=\vec{F}+2\vec{F}=3\vec{F}}$

Solved example 8.13
In fig.8.15(a) below, three equal masses of m kg each are fixed at three corners A, B and D of the square of side a

Fig.8.15

What is the force acting on a mass 1 kg placed at the fourth corner C ?
Solution:
1. Any square will lie on a plane. So this is a 2D problem. We will need the x and y axes only. There is no need for the z-axis
• Assume that, the origin of the coordinate axes is at A. This is shown in fig.b
2. For this square:
(i) C will be equidistant from B and D
C will be at a distance of (2)a from A
3. Now we can begin the calculations:
• The distance vectors are shown in fig.8.16(a) below:

Fig.8.16

• The free body diagram of the 1 kg mass at C is shown in fig.16(b)
4. Force due to mass at B
(i) $\mathbf\small{\vec{F}_{G(B,C)}=-\left[G\frac{m\times 1}{|\vec{r}_{B,C}|^3}\right]\vec{r}_{B,C}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,C)}=-\left[\frac{Gm}{a^3}\right]\vec{r}_{B,C}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{B,C}}$ in component form
• To reach C from B:
    ♦ We have no horizontal distance to travel 
    ♦ We travel only a distance BC vertically up
• So the components of $\mathbf\small{\vec{r}_{B,C}}$ are $\mathbf\small{(0)\hat{i}}$ and $\mathbf\small{a\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{B,C}=a\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(B,C)}=-\left[\frac{Gm}{a^3}\right]a\hat{j}}$
5. Force due to mass at D
(i) $\mathbf\small{\vec{F}_{G(D,C)}=-\left[G\frac{m\times 1}{|\vec{r}_{D,C}|^3}\right]\vec{r}_{D,C}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(D,C)}=-\left[\frac{Gm}{a^3}\right]\vec{r}_{D,C}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{D,C}}$ in component form
• To reach C from D:
    ♦ We have no vertical distance to travel 
    ♦ We travel only a distance DC horizontally to the right
• So the components of $\mathbf\small{\vec{r}_{D,C}}$ are $\mathbf\small{(a)\hat{i}}$ and $\mathbf\small{0\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{D,C}=a\hat{i}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(D,C)}=-\left[\frac{Gm}{a^3}\right]a\hat{i}}$
6. Force due to mass at A:
(i) $\mathbf\small{\vec{F}_{G(A,C)}=-\left[G\frac{m\times 1}{|\vec{r}_{A,C}|^3}\right]\vec{r}_{A,C}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]\vec{r}_{A,C}}$ 
(ii) So our next task is to write $\mathbf\small{\vec{r}_{A,C}}$ in component form
• To reach C from A:
    ♦ First we travel a distance AB horizontally to the right
    ♦ Then we travel a distance BC vertically up
• So the components of $\mathbf\small{\vec{r}_{A,C}}$ are $\mathbf\small{a\hat{i}}$ and $\mathbf\small{a\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{A,C}=a\hat{i}+a\hat{j}}$
(iii) So the result in (i) becomes:
$\mathbf\small{\vec{F}_{G(A,C)}=-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right](a\hat{i}+a\hat{j})}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,C)}=\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{i}\right)+\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{j}\right)}$
7. When we add the results in (4), (5) and (6), we get the net force experienced by the mass at C
So we can write:
The net force experienced by the mass at C
= $\mathbf\small{\vec{F}_{G(B,C)}+\vec{F}_{G(D,C)}+\vec{F}_{G(A,C)}}$
= $\mathbf\small{\left(-\left[\frac{Gm}{a^3}\right]a\hat{j} \right)+\left(-\left[\frac{Gm}{a^3}\right]a\hat{i} \right)+\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{i}\right)+\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{j}\right)}$
(i) First we will add the horizontal terms:
$\mathbf\small{\left(-\left[\frac{Gm}{a^3}\right]a\hat{i} \right)+\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{i}\right)}$
= $\mathbf\small{-\left[\frac{Gm}{a^3}\right]\left(a\hat{i}+\left[\frac{1}{2\sqrt{2}}\right]a\hat{i}\right)}$
= $\mathbf\small{-\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)\hat{i}}$
(ii) Next we add the vertical terms:
$\mathbf\small{\left(-\left[\frac{Gm}{a^3}\right]a\hat{j} \right)+\left(-\left[\frac{Gm}{(\sqrt{2}\,a)^3}\right]a\hat{j}\right)}$
= $\mathbf\small{-\left[\frac{Gm}{a^3}\right]\left(a\hat{j}+\left[\frac{1}{2\sqrt{2}}\right]a\hat{j}\right)}$
= $\mathbf\small{-\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)\hat{j}}$
8. We can write:
■ The resultant force on C has two components:
• The horizontal component is: $\mathbf\small{-\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)\hat{i}}$
• The vertical component is: $\mathbf\small{-\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)\hat{j}}$
9. Note that, the magnitudes of both components are the same
So we can write:
■ The resultant force on C has two components:
• The horizontal component is: $\mathbf\small{-p\hat{i}}$
• The vertical component is: $\mathbf\small{-p\hat{j}}$
Where $\mathbf\small{p=\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)}$
This is shown in fig.8.17(a) below:

Fig.8.17

10. We have two vectors
    ♦ The magnitudes of the two vectors are equal
    ♦ The two vectors are perpendicular to each other
• So the magnitude of the resultant vector will be given by:
$\mathbf\small{\sqrt{p^2+p^2}=\sqrt{2p^2}=\sqrt{2}\;p}$ (Details here)
= $\mathbf\small{\sqrt{2}\left[\frac{Gm}{a^2}\right]\left(1+\frac{1}{2\sqrt{2}}\right)}$
= $\mathbf\small{\left[\frac{Gm}{a^2}\right]\left(\sqrt{2}+\frac{1}{2}\right)}$
• Also, the resultant will be making an angle of 45^o with the horizontal. This is shown in fig.8.17(b)

---

Another method:

• In (6) we wrote: $\mathbf\small{\vec{r}_{A,C}=a\hat{i}+a\hat{j}}$
• We can use trigonometry and write:
$\mathbf\small{\vec{r}_{A,C}=(a\cos45)\hat{i}+(a\sin45)\hat{j}}$
• The reader is advised to write all steps using this alternate method and prove that, the resultant force on the mass at C is the same as that obtained above

---

In the next section, we will see gravitational force of attraction between extended objects

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved

Chapter 8.3 - Gravitational force of Attraction

In the previous section, we saw the Universal law of Gravitation. We saw the method to calculate the magnitude of the force of attraction between two bodies. In this section we will see the details about the direction of that force
1. We have a force of attraction $\mathbf\small{|\vec{F}_G|}$ between two masses m₁ and m₂
• Consider the line joining the 'center of m₁' and 'center of m₂'
■ The $\mathbf\small{|\vec{F}_G|}$ will be acting along this line
• We need to fix up this line mathematically
• For that, we use vectors
2. Fig.8.10 below shows the two masses in 3D space

Fig.8.10

(i) $\mathbf\small{\vec{r}_1}$ is the position vector of m₁
• If we have $\mathbf\small{\vec{r}_1}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m₁ in 3D space (Details here)
(ii) $\mathbf\small{\vec{r}_2}$ is the position vector of m₂
• If we have $\mathbf\small{\vec{r}_2}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get an exact fix on the position of m₂ in 3D space
3. Subtract $\mathbf\small{\vec{r}_2}$ from $\mathbf\small{\vec{r}_1}$
• Remember that, it should be a vector subtraction (Details here)
• The result of this subtraction is $\mathbf\small{\vec{r}_{1,2}}$
• It is the vector pointing from m₁ to m₂
4. We must clearly write about the convention to be followed while writing the distance vector between two masses. We can write it in 3 steps:
(i) There will be two numbers in the subscript
(ii) The first number indicates the mass from which the vector is drawn
    ♦ It is the tail end of the vector
(iii) The second number indicates the mass to which the vector is drawn
    ♦ It is the head end of the vector
5. The vector $\mathbf\small{\vec{r}_{1,2}}$ is our required mathematical fix
If we have $\mathbf\small{\vec{r}_{1,2}}$ in the $\mathbf\small{a\hat{i}+b\hat{j}+c\hat{k}}$ form, we get the exact line through which the $\mathbf\small{\vec{F}_G}$ acts
6. The same $\mathbf\small{|\vec{F}_G|}$ acts on both m₁ and m₂
■ But force on m₁ acts from m₁ towards m₂. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
■ And, force on m₂ acts from m₂ towards m₁. This force is denoted as $\mathbf\small{\vec{F}_{G(1,2)}}$
7. We must clearly write the convention to be followed while writing the force vector between two masses. We can write it in 3 steps: 
(i) There will be two numbers in the subscript
(ii) The first number indicates the 'mass which exerts the pull'
    ♦ The head end of the vector is directed towards this mass
(iii) The second number indicates the 'mass which is being pulled'
    ♦ The tail end of the vector is situated on this mass
8. Now we can write the forces using 'unit vectors'
■ Case 1: The force $\mathbf\small{\vec{F}_{G(2,1)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(2,1)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$ 
• So we get: $\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$ 
(iii) So our next aim is to find the unit vector $\mathbf\small{\hat{r}_{1,2}}$ 
• Clearly, if we divide $\mathbf\small{\vec{r}_{1,2}}$ by it's magnitude, we will get that required unit vector
• That is: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(2,1)}=\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
(v) Note that, the direction of $\mathbf\small{\vec{F}_{G(2,1)}}$ is same as the direction of $\mathbf\small{\vec{r}_{1,2}}$
■ Case 2: The force $\mathbf\small{\vec{F}_{G(1,2)}}$
(i) It's magnitude is given by: $\mathbf\small{|\vec{F}_{G(1,2)}|=G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}}$
(ii) If we multiply this magnitude by the 'unit vector in the direction of $\mathbf\small{\vec{r}_{1,2}}$', the force vector is complete
• This unit vector can be denoted as: $\mathbf\small{\hat{r}_{1,2}}$ 
• So we get: $\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\hat{r}_{1,2}}$
• Note that a negative sign has to be introduced because, direction of $\mathbf\small{\vec{F}_{G(1,2)}}$ is opposite to the direction of $\mathbf\small{\hat{r}_{1,2}}$  
(iii) We have already calculated the unit vector $\mathbf\small{\hat{r}_{1,2}}$ in case 1: $\mathbf\small{\hat{r}_{1,2}=\frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
(iv) So the result in (ii) becomes:
$\mathbf\small{\vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^2}\right]\times \frac{\vec{r}_{1,2}}{|\vec{r}_{1,2}|}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(1,2)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{1,2}|^3}\right]\vec{r}_{1,2}}$
9. Comparing the two cases, we see that:
Magnitudes are the same. The only difference is in direction
• So we can write: $\mathbf\small{\vec{F}_{G(1,2)}=-\vec{F}_{G(2,1)}}$
10. In general, we will be dealing with situations similar to case 2
This can be explained in 5 steps:
(i) Initially, we will be having an object of mass m₁
(ii) We will be asked to find the gravitational force (exerted by m₁) on a new object of mass m₂
(iii) We will be measuring the distance from m₁ to m₂
• So the distance vector will be  $\mathbf\small{\vec{r}_{1,2}}$. Not $\mathbf\small{\vec{r}_{2,1}}$
(iv) The required force will be $\mathbf\small{\vec{F}_{G(1,2)}}$
    ♦ It is the force exerted by m₁ on m₂
    ♦ It will be acting from m₂ towards m₁
(v) So $\mathbf\small{\vec{F}_{G(1,2)}}$ and $\mathbf\small{\vec{r}_{1,2}}$ will be in opposite directions
• Thus the (-)ve sign will be always present. We can write:
Eq.8.2: $\mathbf\small{\vec{F}_G=-\left[G\frac{m_1\; m_2}{|\vec{r}|^3}\right]\vec{r}}$

---

• The above equation 8.2 is applicable to point masses only. In real world, we will be dealing with extended objects. We have already seen the difference between point masses and extended objects in the previous chapter (Details here)
• In the next section, we will see how to apply the equation to extended objects
• Before that, we will see some situations involving point masses only. We will write it in steps:

1. In the fig.8.11 below, we see four point masses m₁, m₂, m₃ and m₄
• They are distributed in a 3D space
• The distances between the 4 masses are denoted by $\mathbf\small{(\vec{r}_{2,1}),\;(\vec{r}_{3,1}),\;\rm{and} \;(\vec{r}_{4,1})}$

Fig.8.11

2. The 4 masses will be exerting forces on each other
■ We want to find the net force experienced by any single mass, say m₁
3. The free body diagram of m₁ is shown in fig.b
• In free body diagrams, we draw only those forces which are acting on the object under consideration. We do not draw those forces which are exerted by the object under consideration
• So we need to draw only those forces which the other masses exert on m₁. We need not consider those forces which m₁ exerts on others
4. We can write the force vectors directly
(i) Force exerted by m₂ on m₁: $\mathbf\small{\vec{F}_{G(2,1)}=-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1}}$
• Based on the conventions that we wrote above, we have:
    ♦ $\mathbf\small{\vec{F}_{G(2,1)}}$ is the force exerted by m₂ on m₁
    ♦ It acts from m₁ towards m₂
    ♦ $\mathbf\small{\vec{r}_{2,1}}$ is the distance vector between m₁ and m₂
    ♦ It is drawn from m₂ to m₁
• So $\mathbf\small{\vec{F}_{G(2,1)}}$ and $\mathbf\small{\vec{r}_{2,1}}$ are in opposite directions. Thus the negative sign becomes necessary in (i) 
• In a similar way, we can write the remaining 2 forces also
(ii) Force exerted by m₃ on m₁: $\mathbf\small{\vec{F}_{G(3,1)}=-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1}}$
(iii) Force exerted by m₄ on m₁: $\mathbf\small{\vec{F}_{G(4,1)}=-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1}}$
• The reader is advised to write 'why the -ve sign becomes necessary in (ii) and (iii)', in his/her own notebooks

5. The net force experienced by m₁ will be the vector sum of the 3 forces written in (4)

So we can write:
Net force experienced $\mathbf\small{\vec{F}_{G}}$ by m₁
= $\mathbf\small{\vec{F}_{G(2,1)}+\vec{F}_{G(3,1)}+\vec{F}_{G(4,1)}}$
= $\mathbf\small{\left(-\left[G\frac{m_1\; m_2}{|\vec{r}_{2,1}|^3}\right]\vec{r}_{2,1} \right)+\left(-\left[G\frac{m_1\; m_3}{|\vec{r}_{3,1}|^3}\right]\vec{r}_{3,1} \right)+\left(-\left[G\frac{m_1\; m_4}{|\vec{r}_{4,1}|^3}\right]\vec{r}_{4,1} \right)}$

---

Now we will see some solved examples

Solved example 8.7
In fig.8.12(a) below, three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC

Fig.8.12

(a) What is the force acting on a mass 2 m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled ?
Take AG = BG = CG = 1 m
Solution:
Part (a):
1. Any triangle will lie on a plane. So this is a 2D problem. We will need the x and y axes only. There is no need for the z-axis
• Assume that, the x-axis passes through the centroid G. Also assume that, the y-axis pass through the top vertex A
• So the two axes will intersect at G
• Thus G will be the origin of the axes. This is shown in fig.b
2. For any equilateral triangle:
(i) G will be equidistant from all the 3 vertices
(ii) Consider any vertex, say C
• The angle BCA at C will be 60^o
• The line CG will bisect the 60^o at that vertex
    ♦ So the angle BCG = 30^o
• So GC will make an angle of 30^o with the horizontal
    ♦ Consequently, GC will make 60^o with the vertical
• In the same way, GB will also make 30^o with the horizontal   
    ♦ Consequently, GB will make 60^o with the vertical
• GA is purely vertical
    ♦ It makes an angle of 90^o with the horizontal
    ♦ It makes 0^o with the vertical
(iii) AG is extended downwards to meet the base BC at D
• Since it is an equilateral triangle, D will be the midpoint of BC
• Also, AD will be perpendicular to BC 
• Since D is the midpoint of BC, the line AD is a median
• The centroid G will divide the median AD in the ratio 2:1
(iv) Consider any vertex
• It's distance from G will be same as for the other two vertices
• So we have: AG = BG = CG
    ♦ In this problem, we are given that AG = BG = CG = 1 m 
3. Now we can begin the calculations:
• The distance vectors are shown in fig.8.13(a) below:

Fig.8.13

• The free body diagram of the 2m mass at G is shown in fig.13(b)
4. Force due to mass at B
(i) $\mathbf\small{\vec{F}_{G(B,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{B,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(B,G)}=-\left[2Gm^2\right]\vec{r}_{B,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{B,G}}$ in component form
• To reach G from B:
    ♦ First we travel a distance BD horizontally to the right
    ♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{B,G}}$ are $\mathbf\small{(BD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{B,G}=(BD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(B,G)}=-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]}$
5. Force due to mass at C
(i) $\mathbf\small{\vec{F}_{G(C,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{B,G}|^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{C,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(C,G)}=-\left[2Gm^2\right]\vec{r}_{C,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{C,G}}$ in component form
• To reach G from C:
    ♦ First we travel a distance CD horizontally to the left
    ♦ Then we travel a distance DG vertically up
• So the components of $\mathbf\small{\vec{r}_{C,G}}$ are $\mathbf\small{-(CD)\hat{i}}$ and $\mathbf\small{(DG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{C,G}=-(CD)\hat{i}+(DG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(CD)\hat{i}+(DG)\hat{j}]}$
(iv) But BD = CD
So the result in (iii) can be written as:
$\mathbf\small{\vec{F}_{G(C,G)}=-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]}$
6. Force due to mass at A
(i) $\mathbf\small{\vec{F}_{G(A,G)}=-\left[G\frac{m\times 2m}{|\vec{r}_{A,G}|^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[G\frac{2m^2}{1^3}\right]\vec{r}_{A,G}}$
$\mathbf\small{\Rightarrow \vec{F}_{G(A,G)}=-\left[2Gm^2\right]\vec{r}_{A,G}}$
(ii) So our next task is to write $\mathbf\small{\vec{r}_{A,G}}$ in component form
• To reach G from A:
    ♦ We have no horizontal distance to travel 
    ♦ We travel only a distance AG vertically down
• So the components of $\mathbf\small{\vec{r}_{A,G}}$ are $\mathbf\small{(0)\hat{i}}$ and $\mathbf\small{-(AG)\hat{j}}$
• We can write: $\mathbf\small{\vec{r}_{A,G}=-(AG)\hat{j}}$
(iii) So the result in (i) becomes: $\mathbf\small{\vec{F}_{G(A,G)}=-\left[2Gm^2\right][-\hat{j}]}$
7. When we add the results in (4), (5) and (6), we get the net force experienced by the mass at G
So we can write:
The net force experienced by the mass at G
= $\mathbf\small{\vec{F}_{G(B,G)}+\vec{F}_{G(C,G)}+\vec{F}_{G(A,G)}}$
= $\mathbf\small{\left(-\left[2Gm^2\right][(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(BD)\hat{i}+(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$ 
• We see that, the two terms with BD will cancel each other. We get:
The net force experienced by the mass at G
= $\mathbf\small{\left([-2Gm^2(DG)\hat{j}]\right)+\left([-2Gm^2(DG)\hat{j}]\right)+\left(-\left[2Gm^2\right][-(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(AG)\hat{j}]\right)}$
8. The centroid G divides the median AD in the ratio 2:1
• That means AG = 2 times DG
• So the result in (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[2Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(4Gm^2[(DG)\hat{j}]\right)=0}$
■ Thus the net force on the mass at G is zero

---

Another method:

• In (4) we wrote: $\mathbf\small{\vec{r}_{B,G}=(BD)\hat{i}+(DG)\hat{j}}$
• We can use trigonometry and thus avoid point D
(Then, we will be able to directly use the given distances: BG, CG and AG) 
• We have: $\mathbf\small{\vec{r}_{B,G}=(BG\cos30)\hat{i}+(BG\sin30)\hat{j}}$
• Similarly, $\mathbf\small{\vec{r}_{C,G}}$ can also be written in terms of angles
• The reader is advised to write all steps using this alternate method and prove that, the net force on the object at G is zero

---

Part (b):
1. In this case, the forces due to B and C are same as in part (a)
• Only change is in the force due to A
• We need to change only the last term in 'part (a)(7)'
2. The interaction is between 'a mass 2m' and 'another mass 2m' 
• So we have (2m × 2m) = 4m²
3. Thus step (7) becomes:
The net force experienced by the mass at G
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(AG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left(\left[4Gm^2\right][(2DG)\hat{j}]\right)}$
= $\mathbf\small{\left([-4Gm^2(DG)\hat{j}]\right)+\left([8Gm^2(DG)\hat{j}]\right)}$
= $\mathbf\small{[4Gm^2(DG)\hat{j}]}$
4. But AG = 2 times DG
• DG = 0.5AG = (0.5 × 1 m) = 0.5 m
• So the result in (3) becomes:
• The net force experienced by the mass at G
= $\mathbf\small{[4Gm^2(0.5)\hat{j}]}$
= $\mathbf\small{[2Gm^2\hat{j}]}$
5. The magnitude of the net force is $\mathbf\small{2Gm^2}$
• It acts in the vertically upward direction

---

• Note that, in part (a), the arrangement of masses is in a symmetrical manner. So the forces cancel out, giving zero net force

• But in part (b), there is no symmetry about the horizontal line passing through G

---

■ The reader is advised to try the alternate method for part (b) also

---

In the next section, we will see a few more solved examples

PREVIOUS           CONTENTS          NEXT

Copyright©2019 Higher Secondary Physics. blogspot.in - All Rights Reserved