In the previous section we saw average velocity and average speed. In this section we will see instantaneous velocity. We will write it in steps:
1. Fig.3.34 below shows a position-time graph of an object:
• In the above graph a point Q is marked. The following two items are clear:
(i) Q is at a distance of 5.12 m from the origin
(ii) The object passed Q when the stop watch showed 4 s
[Note: It is difficult to obtain the value 5.12 from the graph. So we can use the equation of the curve.
The equation is x = 0.08t3.
Substituting t = 4, we get:
s = 0.08 × (4)3= 0.08 × 64 = 5.12]
2. Consider the instant at which the object passed Q
• We want to find the exact velocity at that instant
Let us try:
(i) The point of interest is Q. It is the position of the object when it travelled for 4 seconds
(ii) We need two neighbouring points of Q.
• One before Q and
• The other after Q
(iii) These new points should satisfy a condition:
• They must be at equal time intervals from Q
(iv)Let us choose a point P before Q such that:
♦ The object reached P, 1 s before Q. That is., when the stop watch showed 3 s
• Let us choose a point R after Q such that:
♦ The object reached R, 1 s after Q. That is., when the stop watch showed 5 s
■ So the duration of travel from P to R = Δt = (t2 - t1) = (5 - 3) = 2 s
This is shown in fig.3.35 below:
(v) In the above graph, the distances corresponding to t = 3 and t = 5 are calculated using the same procedure that we used for t = 4:
s(3) = 0.08 × (3)3= 0.08 × 27 = 2.16 m
s(5) = 0.08 × (5)3= 0.08 × 125 = 10 m
(vi) Now we join PR. This is shown in fig.3.36 below:
• Slope of PR can be calculated by completing the triangle PRR'
• We get: Slope of PR = altitude⁄base = RR'⁄PR' = Δx⁄Δt = (10-2.16)⁄(5-3) = 7.84⁄2 = 3.92 ms-1.
(vii) But we know that, this slope gives us only the 'average velocity' between P and R
• Though Q falls between P and R, 3.92 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P to R is 2 s. This '2 s' is not an 'instant'
3. So let us reduce the time interval:
• We need two new neighbouring points of Q. One before Q and the other after Q
• Like before, these new points should also satisfy a condition:
They must be at equal time intervals from Q
(i) Let us choose a point P1 before Q such that:
♦ The object reached P1, 0.5 s before Q. That is., when the stop watch showed 3.5 s
Let us choose a point R1 after Q such that:
♦ The object reached R1, 0.5 s after Q. That is., when the stop watch showed 4.5 s
■ So the duration of travel from P1 to R1 = Δt = (t2 - t1) = (4.5 - 3.5) = 1 s
(ii) After marking P and R, we join them. This is shown in fig.3.37 below:
• In the above graph, the distances corresponding to t = 3.5 and t = 4.5 are calculated using the same procedure that we used for t = 4:
s(3) = 0.08 × (3.5)3= 0.08 × 27 = 3.43
s(5) = 0.08 × (4.5)3= 0.08 × 125 = 7.29
(iii) Slope of P1R1 can be calculated by completing the triangle P1R1R1'
• To avoid congestion, we will zoom in on the required area. This is shown in fig.3.38 below:
• We get: Slope of DF = altitude⁄base = R1R'1 ⁄P1R'1= Δx⁄Δt = (7.29-3.43)⁄(4.5-3.5) = 3.86⁄1 = 3.86 ms-1
(iv) But we know that, this slope gives us only the 'average velocity' between P1 and R1
• Though Q falls between P1 and R1, 3.86 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P1 to R1 is 1 s. This '1 s' is not an 'instant'
4. So let us reduce the time interval:
• We need two new neighbouring points of Q. One before Q and the other after Q
• Like before, these new points should also satisfy a condition:
They must be at equal time intervals from Q
(i) Let us choose a point P2 before Q such that:
♦ The object reached P1, 0.25 s before Q. That is., when the stop watch showed 3.75 s
Let us choose a point R2 after Q such that:
♦ The object reached R2, 0.25 s after Q. That is., when the stop watch showed 4.25 s
■ So the duration of travel from P2 to R2 = Δt = (t2 - t1) = (4.25 - 3.75) = 0.5 s
(ii) After marking P2 and R2, we join them. This is shown in fig.3.39 below. The triangle is also shown:
• We get: Slope of DF = altitude⁄base = R2R'2 ⁄P2R'2
= Δx⁄Δt = (6.1413-4.2188)⁄(4.25-3.75) = 1.9225⁄0.5 = 3.845 ms-1.
(iv) But we know that, this slope gives us only the 'average velocity' between P2 and R2
• Though Q falls between P2 and R2, 3.845 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P2 to R2 is 0.5 s. This '0.5 s' is not an 'instant'
Let us write a summary of what we have done so far:
Step 1: We took points P and R which are centred at 4 s
• The duration of travel (Δt) from P to R was 2 s
• The average velocity with which the object travelled from P to R was 3.92 ms-1
• But the '2 s' is not an instant. So '3.92 ms-1' was discarded
Step 2: We took points P1 and R1 which are centred at 4 s
• The duration of travel (Δt) from P1 to R1 was 1 s
• The average velocity with which the object travelled from P1 to R1 was 3.86 ms-1
• But the '1 s' is not an instant. So '3.86 ms-1' was discarded
Step 3: We took points P2 and R2 which are centred at 4 s
• The duration of travel (Δt) from P2 to R2 was 0.5 s
• The average velocity with which the object travelled from P2 to R2 was 3.845 ms-1
• But the '0.5 s' is not an instant. So '3.845 ms-1' was discarded
• From the above 3 steps, it is clear that, with each step, the following two items are decreasing:
♦ Distance between P and R
♦ Time duration required for the travel between P and R
This can be shown as in fig.3.40 below:
• We can see that, the lines are becoming more and more aligned with the curve
• We must continue the steps until the time of travel between P and R is very small
• But it is not convenient to use graphs for further steps. because, the points will be very close to each other. We can use a table to do the calculations. It is shown below:
• The three steps that we already did are given in the first 3 rows of the table.
• Two more steps are done in the table. In the fifth step, Δt is very small. It is 0.01
■ But even this is not sufficient. Let us see the reason:
• Consider the ratio Δx⁄Δt . We know that this ratio gives the average velocity
• To get the instantaneous velocity, the denominator Δt must be very small (like 0.00000001 s)
• It must be very small. We call it: 'infinitesimal time' . The meaning of 'infinitesimal' can be seen here.
♦ And at the same time, it must not be equal to zero. Because, division by zero is undefined
• Mathematically, such a small denominator is indicated as: 'Δx⁄Δt when Δt → 0'
♦ That is.,we need the ratio when 'Δt tends to zero'
• Such a ratio can be easily calculated using the principles of calculus which we will study in maths classes.
• The reader may try to write the answer after learning calculus. The answer will be obtained as 3.84 ms-1.
We know that, 'Δx⁄Δt' is a slope.
• When we use calculus, we get a value of Δx⁄Δt
♦ (The value of the ratio when the denominator Δt is very small)
• This value of the ratio, 'when Δt is very small', is also a slope
• It is the slope of the tangent to the curve at the point where we seek the instantaneous velocity
• The lines PR, P1R1, P2R2 etc., touches the curve at two points
• But the tangent will touch the curve only at one point, which is Q
Another example:
In the above example, the equation of motion was x = 0.08t3. We used this equation to find the distances at various times. Now consider an object moving according to the equation:
x = 8.5 + 2.5t2.
• What is the instantaneous velocity at t = 0 s ?
• What is the instantaneous velocity at t = 2 s ?
• What is the average velocity with which it travels between t = 2 and t = 4 s
Solution:
A. To find instantaneous velocities:
1. Based on the principles of calculus, the ratio 'Δx⁄Δt when Δt → 0' is: 5t.
2. So we get:
• At t = 0, the instantaneous velocity = 5 × 0 = 0 ms-1
• At t = 2, the instantaneous velocity = 5 × 2 = 10 ms-1
B. To find average velocity:
1. Distance travelled when t = 2 s
= x(2) = (8.5 + 2.5×(2)2) = 18.5 m
• Distance travelled when t = 4 s
= x(4) = (8.5 + 2.5×(4)2) = 48.5 m
2. So Δx = (48.5 - 18.5) = 30
• Δt = (t2 - t1) = (4 - 2) = 2 s
3. Average velocity = Δx⁄Δt = 30⁄2 = 15 ms-1.
1. Fig.3.34 below shows a position-time graph of an object:
 |
| Fig.3.34 |
(i) Q is at a distance of 5.12 m from the origin
(ii) The object passed Q when the stop watch showed 4 s
[Note: It is difficult to obtain the value 5.12 from the graph. So we can use the equation of the curve.
The equation is x = 0.08t3.
Substituting t = 4, we get:
s = 0.08 × (4)3= 0.08 × 64 = 5.12]
2. Consider the instant at which the object passed Q
• We want to find the exact velocity at that instant
Let us try:
(i) The point of interest is Q. It is the position of the object when it travelled for 4 seconds
(ii) We need two neighbouring points of Q.
• One before Q and
• The other after Q
(iii) These new points should satisfy a condition:
• They must be at equal time intervals from Q
(iv)Let us choose a point P before Q such that:
♦ The object reached P, 1 s before Q. That is., when the stop watch showed 3 s
• Let us choose a point R after Q such that:
♦ The object reached R, 1 s after Q. That is., when the stop watch showed 5 s
■ So the duration of travel from P to R = Δt = (t2 - t1) = (5 - 3) = 2 s
This is shown in fig.3.35 below:
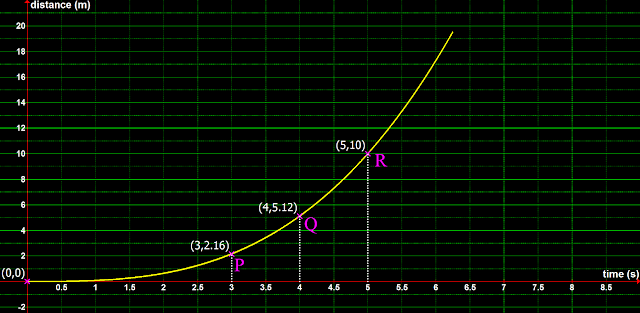 |
| Fig.3.35 |
s(3) = 0.08 × (3)3= 0.08 × 27 = 2.16 m
s(5) = 0.08 × (5)3= 0.08 × 125 = 10 m
(vi) Now we join PR. This is shown in fig.3.36 below:
 |
| Fig.3.36 |
• We get: Slope of PR = altitude⁄base = RR'⁄PR' = Δx⁄Δt = (10-2.16)⁄(5-3) = 7.84⁄2 = 3.92 ms-1.
(vii) But we know that, this slope gives us only the 'average velocity' between P and R
• Though Q falls between P and R, 3.92 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P to R is 2 s. This '2 s' is not an 'instant'
3. So let us reduce the time interval:
• We need two new neighbouring points of Q. One before Q and the other after Q
• Like before, these new points should also satisfy a condition:
They must be at equal time intervals from Q
(i) Let us choose a point P1 before Q such that:
♦ The object reached P1, 0.5 s before Q. That is., when the stop watch showed 3.5 s
Let us choose a point R1 after Q such that:
♦ The object reached R1, 0.5 s after Q. That is., when the stop watch showed 4.5 s
■ So the duration of travel from P1 to R1 = Δt = (t2 - t1) = (4.5 - 3.5) = 1 s
(ii) After marking P and R, we join them. This is shown in fig.3.37 below:
 |
| Fig.3.37 |
s(3) = 0.08 × (3.5)3= 0.08 × 27 = 3.43
s(5) = 0.08 × (4.5)3= 0.08 × 125 = 7.29
(iii) Slope of P1R1 can be calculated by completing the triangle P1R1R1'
• To avoid congestion, we will zoom in on the required area. This is shown in fig.3.38 below:
 |
| Fig.3.38 |
(iv) But we know that, this slope gives us only the 'average velocity' between P1 and R1
• Though Q falls between P1 and R1, 3.86 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P1 to R1 is 1 s. This '1 s' is not an 'instant'
4. So let us reduce the time interval:
• We need two new neighbouring points of Q. One before Q and the other after Q
• Like before, these new points should also satisfy a condition:
They must be at equal time intervals from Q
(i) Let us choose a point P2 before Q such that:
♦ The object reached P1, 0.25 s before Q. That is., when the stop watch showed 3.75 s
Let us choose a point R2 after Q such that:
♦ The object reached R2, 0.25 s after Q. That is., when the stop watch showed 4.25 s
■ So the duration of travel from P2 to R2 = Δt = (t2 - t1) = (4.25 - 3.75) = 0.5 s
(ii) After marking P2 and R2, we join them. This is shown in fig.3.39 below. The triangle is also shown:
 |
| Fig.3.39 |
= Δx⁄Δt = (6.1413-4.2188)⁄(4.25-3.75) = 1.9225⁄0.5 = 3.845 ms-1.
(iv) But we know that, this slope gives us only the 'average velocity' between P2 and R2
• Though Q falls between P2 and R2, 3.845 ms-1 is not the instantaneous velocity at Q
• The duration of travel from P2 to R2 is 0.5 s. This '0.5 s' is not an 'instant'
Let us write a summary of what we have done so far:
Step 1: We took points P and R which are centred at 4 s
• The duration of travel (Δt) from P to R was 2 s
• The average velocity with which the object travelled from P to R was 3.92 ms-1
• But the '2 s' is not an instant. So '3.92 ms-1' was discarded
Step 2: We took points P1 and R1 which are centred at 4 s
• The duration of travel (Δt) from P1 to R1 was 1 s
• The average velocity with which the object travelled from P1 to R1 was 3.86 ms-1
• But the '1 s' is not an instant. So '3.86 ms-1' was discarded
Step 3: We took points P2 and R2 which are centred at 4 s
• The duration of travel (Δt) from P2 to R2 was 0.5 s
• The average velocity with which the object travelled from P2 to R2 was 3.845 ms-1
• But the '0.5 s' is not an instant. So '3.845 ms-1' was discarded
• From the above 3 steps, it is clear that, with each step, the following two items are decreasing:
♦ Distance between P and R
♦ Time duration required for the travel between P and R
This can be shown as in fig.3.40 below:
 |
| Fig.3.40 |
• We must continue the steps until the time of travel between P and R is very small
• But it is not convenient to use graphs for further steps. because, the points will be very close to each other. We can use a table to do the calculations. It is shown below:
• The three steps that we already did are given in the first 3 rows of the table.
• Two more steps are done in the table. In the fifth step, Δt is very small. It is 0.01
■ But even this is not sufficient. Let us see the reason:
• Consider the ratio Δx⁄Δt . We know that this ratio gives the average velocity
• To get the instantaneous velocity, the denominator Δt must be very small (like 0.00000001 s)
• It must be very small. We call it: 'infinitesimal time' . The meaning of 'infinitesimal' can be seen here.
♦ And at the same time, it must not be equal to zero. Because, division by zero is undefined
• Mathematically, such a small denominator is indicated as: 'Δx⁄Δt when Δt → 0'
♦ That is.,we need the ratio when 'Δt tends to zero'
• Such a ratio can be easily calculated using the principles of calculus which we will study in maths classes.
• The reader may try to write the answer after learning calculus. The answer will be obtained as 3.84 ms-1.
We know that, 'Δx⁄Δt' is a slope.
• When we use calculus, we get a value of Δx⁄Δt
♦ (The value of the ratio when the denominator Δt is very small)
• This value of the ratio, 'when Δt is very small', is also a slope
• It is the slope of the tangent to the curve at the point where we seek the instantaneous velocity
• The lines PR, P1R1, P2R2 etc., touches the curve at two points
• But the tangent will touch the curve only at one point, which is Q
Another example:
In the above example, the equation of motion was x = 0.08t3. We used this equation to find the distances at various times. Now consider an object moving according to the equation:
x = 8.5 + 2.5t2.
• What is the instantaneous velocity at t = 0 s ?
• What is the instantaneous velocity at t = 2 s ?
• What is the average velocity with which it travels between t = 2 and t = 4 s
Solution:
A. To find instantaneous velocities:
1. Based on the principles of calculus, the ratio 'Δx⁄Δt when Δt → 0' is: 5t.
2. So we get:
• At t = 0, the instantaneous velocity = 5 × 0 = 0 ms-1
• At t = 2, the instantaneous velocity = 5 × 2 = 10 ms-1
B. To find average velocity:
1. Distance travelled when t = 2 s
= x(2) = (8.5 + 2.5×(2)2) = 18.5 m
• Distance travelled when t = 4 s
= x(4) = (8.5 + 2.5×(4)2) = 48.5 m
2. So Δx = (48.5 - 18.5) = 30
• Δt = (t2 - t1) = (4 - 2) = 2 s
3. Average velocity = Δx⁄Δt = 30⁄2 = 15 ms-1.
In the next section, we will see acceleration.
Copyright©2018 Higher Secondary Physics. blogspot.in - All Rights Reserved

No comments:
Post a Comment