In the previous section we saw acceleration. We also saw that, velocity-time graph of an object moving with constant acceleration will be a straight line. In this section we will see the different orientations possible for such straight line graphs.
1. Consider the velocity-time graph shown below:
• The inclined pink line is the velocity-time graph
2. The coordinates of some random points are marked on the graph.
• At the instant when the experiment was begun (t= 0), the object was moving with a velocity of 80 ms-1.
• After 1 s (t= 1), the velocity became 71 ms-1
• After 1 more second (t = 2), the velocity became 62 ms-1.
• So, with the passage of time, the velocity is decreasing
3. We know that the body was moving with uniform acceleration (∵ the graph is a straight line)
The value of this acceleration can be calculated using the triangle AA'B
• We have: Slope of the pink line = altitude⁄base
• Altitude in numerator = AA' = Δv = (v2 - v1) = (39.5 - 62) = -22.5
• Base in denominator = A'B = Δt = (t2 - t1) = (4.5 - 2) = 2.5
• Thus slope = AA'⁄A'B = Δv⁄Δt = -22.5⁄2.5 = -9 ms-2.
4. We get a -ve value for acceleration. Why is that so?
Ans: With the passage of time, velocity is decreasing.
• That means, the acceleration is acting in the direction opposite to that of the velocity.
• So indeed acceleration will be negative in this case
■ We can write the general case:
If the object moves with a 'uniform negative acceleration', the velocity-time graph will be a falling line
■ The converse is also applicable:
If the given velocity-time graph is a falling line, then the object was moving with a 'uniform negative acceleration'. That is., the object as slowing down at a uniform rate
5. We started this experiment at the instant when the object passed a convenient point
• The stop watch was turned on at that instant
• The velocity of the object was 80 ms-1 at that instant
5. Let us write the relation to coordinate geometry:
• Equation of the pink line is:
v = at + 80
'a' has a negative value: -9
So the equation is: v = -9t + 80
6. Using this equation, we can find the time at which the body will come to rest.
• For that, we put v = 0
• Thus we get: 0 = -9t + 80
⟹ 9t = 80 ⟹ t = 8.9 s
• If we extend the pink line in fig.3.44 downwards, it will meet the time axis at (8.9,0)
Now we will see another orientation.
1. Consider the velocity-time graph shown below:
• The pink line is below the time axis
• All the y coordinates are negative
• That means, the object moved with a negative velocity
• 'Negative velocity' indicates that, the object was moving towards the negative side of the x axis
2. Note that, even though it was moving towards the negative side of the x axis, it was having positive acceleration. That is., the velocity of the body was increasing every instant.
• This is clear because, the graph is a rising line
1. Consider a velocity-time graph shown below:
• The pink line is below the time axis
• All the y coordinates are negative
• That means, the object moved with a negative velocity
• 'Negative velocity' indicates that, the object was moving towards the negative side of the x axis
2. Note that,it was moving towards the negative side of the x axis and at the same time, it was having negative acceleration. That is., the velocity of the body was decreasing every instant.
• This is clear because, the graph is a falling line
We will see one more orientation.
1. Consider the velocity-time graph shown below:
• Part of the pink line is above the time axis The rest is below the time axis
• Above the time axis, all the y coordinates are positive.
♦ Below the time axis, all the y coordinates are negative
• That means, initially, the object moved with a positive velocity.
♦ After some it moved with negative velocity
2. How is that possible?
Let us analyse:
(i) Consider the point of intersection of the pink line with the x axis. The coordinates are: (3.67,0)
(ii) The object was moving with positive velocity until the stop watch showed 3.67 s
(iii) After that it moved with negative velocity
3. So it is clear:
• The object was moving towards the positive side of the x axis until the stop watch showed 3.67 s
• After that, it changed direction. It began to move in the exact opposite direction. That is., towards the negative side of the x axis
3. Note that, during the entire journey, it was having negative acceleration.
• This is clear because, the graph is a falling line
Now we will see an application of the velocity-time graph
1. Consider the velocity time graph shown below:
• It is clear that the object moved with uniform velocity of 'u' ms-1. There was no acceleration
2. Consider the following two instants:
• Instant at which the stop watch showed t1 seconds. It is marked as P
• Instant at which the stop watch showed t2 seconds. It is marked as Q
3. Draw vertical lines at P and Q
• These vertical lines intersect the velocity-time graph at P' and Q'
4. Now calculate the area of the rectangle PQQ'P'. We get:
• Area = (PP' × PQ) = u(t2 - t1)
5. In the right side of the above equation, we are multiplying two quantities:
(i) velocity
(ii) a time duration.
• We know that, when we multiply those two quantities, we get the 'displacement in that duration'
■ So the 'area below the above velocity-time graph' is the 'displacement of the object'
• The above velocity-time graph is horizontal. So it was easy to calculate the area
• Is it true for all types of velocity-time graphs? Let us try:
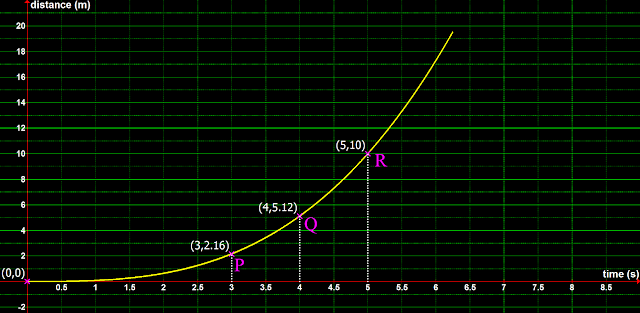
1. Consider the velocity time graph shown below:
• It is clear that the object moved with uniform acceleration
2. Consider the following two instants:
• Instant at which the stop watch showed t1 seconds. It is marked as P
• Instant at which the stop watch showed t2 seconds. It is marked as Q
3. Draw vertical lines at P and Q
• These vertical lines intersect the velocity-time graph at P' and Q'
• We have a trapezium PQQ'P'.
• It's area can be calculated by splitting it into a rectangle and a triangle
4. Using the principles of calculus, we can prove that, this area is equal to:
The displacement of the object in the duration (t2 - t1)
• We saw some basics about this proof here.
■ So we can write the general form:
The area enclosed between a velocity-time graph and the x axis will give the displacement of the object
1. Consider the velocity-time graph shown below:
 |
| Fig.3.44 |
2. The coordinates of some random points are marked on the graph.
• At the instant when the experiment was begun (t= 0), the object was moving with a velocity of 80 ms-1.
• After 1 s (t= 1), the velocity became 71 ms-1
• After 1 more second (t = 2), the velocity became 62 ms-1.
• So, with the passage of time, the velocity is decreasing
3. We know that the body was moving with uniform acceleration (∵ the graph is a straight line)
The value of this acceleration can be calculated using the triangle AA'B
• We have: Slope of the pink line = altitude⁄base
• Altitude in numerator = AA' = Δv = (v2 - v1) = (39.5 - 62) = -22.5
• Base in denominator = A'B = Δt = (t2 - t1) = (4.5 - 2) = 2.5
• Thus slope = AA'⁄A'B = Δv⁄Δt = -22.5⁄2.5 = -9 ms-2.
4. We get a -ve value for acceleration. Why is that so?
Ans: With the passage of time, velocity is decreasing.
• That means, the acceleration is acting in the direction opposite to that of the velocity.
• So indeed acceleration will be negative in this case
■ We can write the general case:
If the object moves with a 'uniform negative acceleration', the velocity-time graph will be a falling line
■ The converse is also applicable:
If the given velocity-time graph is a falling line, then the object was moving with a 'uniform negative acceleration'. That is., the object as slowing down at a uniform rate
5. We started this experiment at the instant when the object passed a convenient point
• The stop watch was turned on at that instant
• The velocity of the object was 80 ms-1 at that instant
5. Let us write the relation to coordinate geometry:
• Equation of the pink line is:
v = at + 80
'a' has a negative value: -9
So the equation is: v = -9t + 80
6. Using this equation, we can find the time at which the body will come to rest.
• For that, we put v = 0
• Thus we get: 0 = -9t + 80
⟹ 9t = 80 ⟹ t = 8.9 s
• If we extend the pink line in fig.3.44 downwards, it will meet the time axis at (8.9,0)
Now we will see another orientation.
1. Consider the velocity-time graph shown below:
 |
| Fig.3.45 |
• All the y coordinates are negative
• That means, the object moved with a negative velocity
• 'Negative velocity' indicates that, the object was moving towards the negative side of the x axis
2. Note that, even though it was moving towards the negative side of the x axis, it was having positive acceleration. That is., the velocity of the body was increasing every instant.
• This is clear because, the graph is a rising line
1. Consider a velocity-time graph shown below:
 |
| Fig.3.46 |
• All the y coordinates are negative
• That means, the object moved with a negative velocity
• 'Negative velocity' indicates that, the object was moving towards the negative side of the x axis
2. Note that,it was moving towards the negative side of the x axis and at the same time, it was having negative acceleration. That is., the velocity of the body was decreasing every instant.
• This is clear because, the graph is a falling line
We will see one more orientation.
1. Consider the velocity-time graph shown below:
 |
| Fig.3.47 |
• Above the time axis, all the y coordinates are positive.
♦ Below the time axis, all the y coordinates are negative
• That means, initially, the object moved with a positive velocity.
♦ After some it moved with negative velocity
2. How is that possible?
Let us analyse:
(i) Consider the point of intersection of the pink line with the x axis. The coordinates are: (3.67,0)
(ii) The object was moving with positive velocity until the stop watch showed 3.67 s
(iii) After that it moved with negative velocity
3. So it is clear:
• The object was moving towards the positive side of the x axis until the stop watch showed 3.67 s
• After that, it changed direction. It began to move in the exact opposite direction. That is., towards the negative side of the x axis
3. Note that, during the entire journey, it was having negative acceleration.
• This is clear because, the graph is a falling line
Now we will see an application of the velocity-time graph
1. Consider the velocity time graph shown below:
 |
| Fig.3.48 |
2. Consider the following two instants:
• Instant at which the stop watch showed t1 seconds. It is marked as P
• Instant at which the stop watch showed t2 seconds. It is marked as Q
3. Draw vertical lines at P and Q
• These vertical lines intersect the velocity-time graph at P' and Q'
4. Now calculate the area of the rectangle PQQ'P'. We get:
• Area = (PP' × PQ) = u(t2 - t1)
5. In the right side of the above equation, we are multiplying two quantities:
(i) velocity
(ii) a time duration.
• We know that, when we multiply those two quantities, we get the 'displacement in that duration'
■ So the 'area below the above velocity-time graph' is the 'displacement of the object'
• The above velocity-time graph is horizontal. So it was easy to calculate the area
• Is it true for all types of velocity-time graphs? Let us try:
1. Consider the velocity time graph shown below:
 |
| Fig.3.49 |
2. Consider the following two instants:
• Instant at which the stop watch showed t1 seconds. It is marked as P
• Instant at which the stop watch showed t2 seconds. It is marked as Q
3. Draw vertical lines at P and Q
• These vertical lines intersect the velocity-time graph at P' and Q'
• We have a trapezium PQQ'P'.
• It's area can be calculated by splitting it into a rectangle and a triangle
4. Using the principles of calculus, we can prove that, this area is equal to:
The displacement of the object in the duration (t2 - t1)
• We saw some basics about this proof here.
■ So we can write the general form:
The area enclosed between a velocity-time graph and the x axis will give the displacement of the object
In the next section, we will see the equations of motion.
Copyright©2018 Higher Secondary Physics. blogspot.in - All Rights Reserved